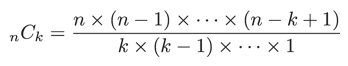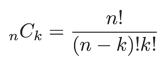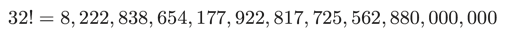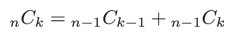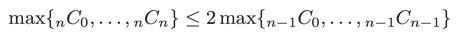SRM 535 Div II
SRM 535 Div II
- 初参加したSRMにて惨敗した問題に挑戦。今でも自分には中々難しく、35分ほど時間を要した
FromAndGCDLCM
- 未知の数AとBの最大公約数と最小公倍数、GとLが与えられる。ここからAとBを推測し、その最小の和(A + B)を返す問題
- 最大公約数Gと最小公倍数Lに有効なAとBが存在しなければ-1を返す
- 問題を見てまずぱっと思い浮かべた式は以下だ
- AとBは[1, 1012]を取る値だ。そのため、上述の左辺が1024を取りうる。これは約1,0008、約280の値だ。素直に実装したらlong longから溢れてしまう
- さて、上述の式を変形すると、以下となる。
- 問題に習い、lcm(A, B)L、gcd(A, B)をGとすると、右辺はLGとすることが出来る。
- AとBを乗してLGとなるようなAとBの組み合わせを求めるような実装は大抵、以下のような形となることが多い。計算量はO(√LG)だ
for (int i = 1; i * i <= LG; i ++) :
- さて、この場合、AはGの倍数である。またlong longであることを加味すると、つまり、この実装は以下のような形になると思われる
for (long long A = G; A * A <= LG; G ++) :
- LGがlong longに納まりきらないことを承知の上で実装を進めると、以下となる(最大公約数を今一度求めるのは実装をテストして気付いた。サンプルになければWAを出していたところだ)
long long nm = INF; for (long long A = G; A * A <= LG; G ++) if (LG % A == 0) { long long B = LG / A; if (std::__gcd(A, B) == G) nm = std::min(A + B, nm); }
- 繰り返すが、A・AやLGはlong longに収まらない。そのため、何らかの回避策を取る必要がある
- AをiGと表すことにする。iを倍数として、long longから溢れさせないようにする作戦だ
- 難しいのは反復の条件だ。A = iGとすると、以下とすることができる
- また、iからBを求めるには以下とする
- これらを用い、上述の実装をリファクタリングして、以下とすることができる
long long nm = INF; for (long long i = 1; i * i <= L / G; i ++) { long long A = i * G; if (L % i == 0) { long long B = L / i; if (std::__gcd(A, B) == G) nm = std::min(A + B, nm); } }
まとめ
- SRM参戦時に惨敗した問題。解けて素直に嬉しく思うと共に、Div II Mediumとしてはなかなか難しく、またとても良問であったように思えた
- A、B、lcm(A, B)、gcd(A, B)を考えるとき、以下の関係式は大変重宝する
- 積がNとなるようなiとjを組み合わせる際の典型の実装は以下となり、その計算量はO(√N)である
for (int i = 1; i * i <= N; i ++) if (N % i == 0) { int j = N / i; : }
SRM 653 Div I
SRM 653 Div I
http://community.topcoder.com/stat?c=round_overview&er=5&rd=16317
SRM 653 Div Iに参加。制限時間一杯Easyを考えるが、全く手が出ず。SRM後に幾つかの実装を読み、全く考えもしていなかった問題に還元できることを学んだ。
グラフの問題であると捉え作図を行ったため、メモの代わりとしてブログ記事として記載した。
CountryGroupHard
http://community.topcoder.com/stat?c=problem_statement&pm=13688&rd=16317
- 以下のような数の並びが与えられる
- 数値の周りには同じ数値が、数値分だけ集まる
- 0は数値が隠されていることを示す
- 1以上の数値は既知であることを示し、必ず正しい
- 全体が成立するように、数値を推定したい
- そのとき既知の数値から隠された数値を一意に推定できるかどうかを判断して回答する問題
- 例えばこの例は数値が一意に求まり、以下のようなものであったと推定できる
- 以下も数値が一意に求まる例だ
- 以下は数値が一意に求まらない例
- この数列を成立させる組み合わせは複数ある。書き出してみると5種類あった
- SRM終了後に幾つかの実装を読み、ようやく理解をすることができた
- 自分が理解する上で一番しっくりきたのが、経路の組み合わせを数え上げる問題に還元するものであった
- 先ほどの例で考えてみよう。数値の列として捉えるのではなく、
- 以下のように成立する経路を考え、その経路を数え上げる問題とするような感覚で捉えるのが自分には合っているらしい
- さて、実際には上記のように極度に抽象化したグラフではなく、数値群の間に頂点を配置して考えた
- 初期状態では左端の頂点にのみ経路が設定されていることに注意したい。またその数は1だ
- 一番左の数値に1を設定してみよう。結果、左端の頂点から次の頂点への経路が成立する。つまり、左端の頂点から次の頂点への経路は少なくとも1種類存在すると言える
- そのため、二つ右側への頂点へ左端の頂点に到達する経路の数、1を足し込む
- 一番左の数値に2を設定してみよう。このときは左端の頂点から二つ右側への頂点への経路が成立する。先ほどと同様に、左端の頂点から二つ右側への頂点への経路は1種類存在すると言える
- そのため、二つ右側への頂点へ左端の頂点に到達する経路の数、1を足し込む
- 一番左の数値に3を設定してみよう。3の周辺には3つの3が集まるはずだが、隣の数値は2で、条件が成立しない。そのため、経路も成立せず、この場合は左端の頂点から三つ右側への頂点への経路が存在しないことが分かる
- 左側の頂点からの経路をまとめてみよう。以下のようになる
- 二つ目の頂点から同様に考える。しかし、この頂点から成立する経路がない
- 三つ目の頂点からも考えてみよう。以下のように右側の数値群を3で埋めてやると経路が成立することが分かる
- 三つ目の頂点からの経路をまとめる
- 四つ目の頂点からの経路を考える。四つ目の頂点からの経路は成立するのだが、そもそも左端の頂点から四つ目の頂点に到達する経路がないため、最終的な経路の組み合わせ数に寄与しない
- 五つ目の頂点からの経路も同様に寄与しない
- 結果、左端の頂点から右端の頂点への経路は1種類しかないと言え、問題の答えも一意に推定できるものとすることができる。以下は左端から右端の頂点までの経路をまとめたものだ
- 以下は成立する例
- その経路をまとめたもの
- 以下は成立しない例
- 結果、左端の頂点から右端の頂点へ到達しうる経路は5種類であることが分かる
- 確かに書き下した組み合わせの数も5種類であった
おまけ
class CountryGroupHard {
public:
std::string solve(std::vector<int> a) {
int size = a.size();
long long dp[111] = {0};
dp[0] = 1;
For (int i = 0; i < size; i ++)
for (int j = 1; i + j <= size; j ++) {
bool valid = true;
for (int k = 0; k < j; k ++)
if (a[i + k] && a[i + k] != j)
valid = false;
if (valid)
dp[i + j] = (dp[i + j] + dp[i]) % MOD;
}
return dp[size] == 1 ? "Sufficient" : "Insufficient";
};
};
マラソンマッチにおける典型データ構造とアプローチ
TopCoderのマラソンマッチは大きく以下の二つの形式に分類することができます。
- 最適化
- 機会学習
何れの形式のマッチもそれぞれの魅力的がありますが、今回は特に最適化に主眼を置いたマッチを題材にお話しをします。最適化を主眼においたマッチがどのようなものであるか、2013年の12月に開催されたMM 82を用いて簡単に紹介します。ColorLinkerという問題です。
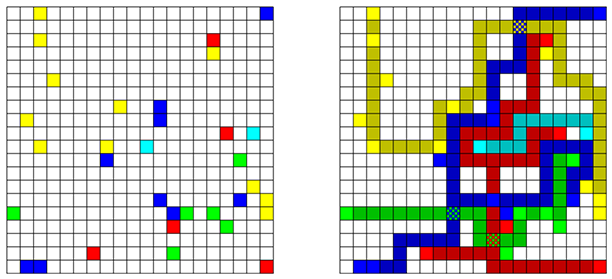
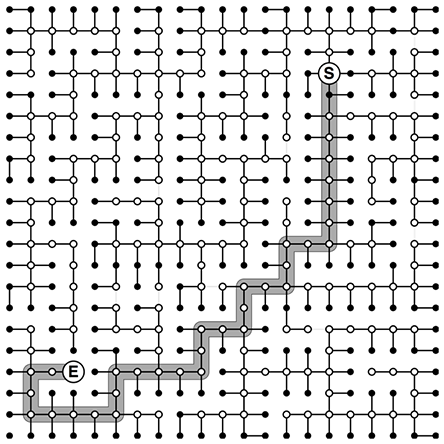
プログラムには正方形のグリッドが与えられます。グリッドのいくつかのセルは予め彩色がなされています。
我々に与えられた課題は、同じ色のセルが全て繋がるように空のセルを彩色していくことです。セルを彩色するにはコストがかかります。また、同一のセルを複数色に彩色するとコストは指数的に増加します。合計のコストが低ければ低いほどよい彩色であると評価されます。同じ色のセルが連結でない場合は無効となります。
この問題に対する典型的なアプローチの一つは最短経路探索、特に複数始点から同時にダイクストラ法を適用し焼きなましを行う、というものであったようです。
さて、TopCoderの最適化問題ではこのようにシンプルな二次元グリッドの問題がほどよい頻度で出題されます。そのため、二次元グリッドを効率よく扱うことはTopCoderのマラソンマッチに参加する上で必須のテクニックであると言えます。このエントリでは、TopCoderマラソンマッチにおける典型データ構造とアプローチを主題に以下のトピックに精選し、紹介したいと思います。
- 盤面の持ちかたと最短経路探索
- キュー
- 経路復元
- コスト付き最短経路探索
盤面の持ちかたと最短経路探索
まず初めに盤面の持ちかたについて考えてみましょう。実際のマラソンマッチの問題は過分に複雑なので、これを模した問題を用意することにします。
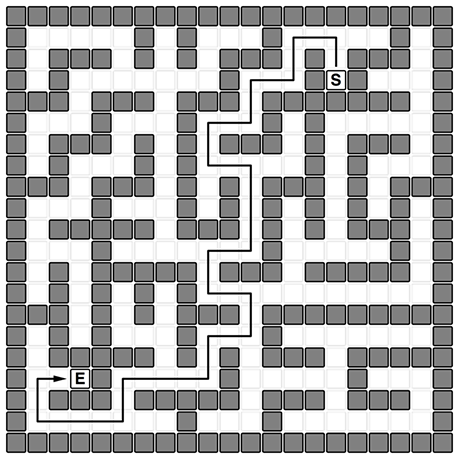
迷路が与えられます。迷路は通路と壁で構成されています。その後3秒の間、二点がランダムに、繰り返し与えられます。この二点間の最短経路を出来るだけ速く探索するメソッドを書くのを目標とすることとします。説明やサンプルプログラムを簡単にするために、このプログラムは最短距離の長さも経路も返しません。もはや問題とはなっていませんが、ご容赦ください。
さて、目的のクラス名をsolver_tとしましょう。このクラスは以下のような二つのメソッドを持つものとします。
void solver_t::init(const std::vector<std::string>& a); void solver_t::bfs(int sx, int sy, int ex, int ey);
initメソッドにはいわゆる「迷路」が渡されます。迷路がプログラムに渡されるのは初めの1回だけとします。データは、std::stringのstd::vectorとします。パウンド(#)が壁、ピリオド(.)が通路を表します。迷路の縦と横の長さは等しくNとします。Nの範囲は毎回異なり、15〜55としましょう。迷路生成の都合から、Nは奇数とします。範囲外には外壁があるものとします。
実際の迷路のデータを覗いてみましょう。競技プログラミングではよく見る感じのデータですので、慣れているかたも多いのではないでしょうか。
.....#.#...#.....#. .###.#.#.###.#.###. .#.......#...#.#... ##.###.###.#######. ...#...#...#.#..... .###.#.#.###.#.###. .#...#.#.....#.#... ##.###.#.#.###.#.## ...#...#.#.#.#.#.#. .#####.###.#.#.###. ...#.......#.....#. .#.#####.###.#####. .#.#.#.#........... ##.#.#.###.######## .#.#...#...#....... .#####.#.#.###.#### ...#.....#.....#... .###.#####.###.###. .......#...#.......
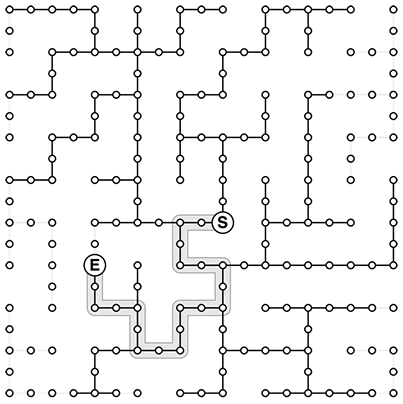
bfsメソッドには開始点と終了点が渡されます。そこから以下のような最短経路を探索したい、ということです。
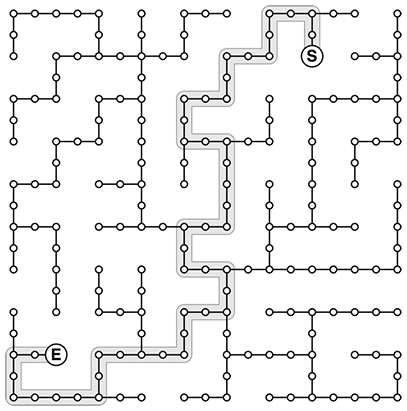
この問題を計算機で解く際はグラフの問題として捉えると便利なことがあります。その様子を少し覗いておきましょう。通路を頂点と置き換え、隣接した頂点間に辺を張ります。
さて、bfsメソッドという名前が諮詢しているように、我々の仕事は速い幅優先探索を書くことです...
では早速実装を開始します。迷路のデータはSTLを使って渡されることですし、そのままデータとして使うことにします。
クラスの定義はこのような感じになるでしょうか。
class solver_t { pubilc: void init(const std::vector<std::string>& a); void bfs(int sx, int sy, int ex, int ey); private: std::vector<std::string> a_; int N_; std::vector<std::vector<bool>> visit_; };
solver_t::init()では盤面をそのまま保持します。また、盤面の大きさに伴ったvisit_変数を確保しておきましょう。
void solver_t::init(const std::vector<std::string>& a) { a_ = a; N_ = a_.size(); visit_.assign(N_, std::vector<bool>(N_)); };
最後にbfs()メンバ関数を記述します。とてもオーソドックスな幅優先探索の実装です。
void solver_t::bfs(int sx, int sy, int ex, int ey) { for (int i = 0; i < N_; i ++) for (int j = 0; j < N_; j ++) visit_[i][j] = false; visit_[sy][sx] = true; std::queue<int> queue; queue.push(XY(sx, sy)); while (! queue.empty()) { int p = queue.front(); queue.pop(); int x = X(p); int y = Y(p); for (int k = 0; k < 4; k ++) { int xx = x + dx[k], yy = y + dy[k]; if (0 <= xx && xx < N_ && 0 <= yy && yy < N_) { if (xx == ex && yy == ey) return; if (! visit_[yy][xx]) if (a_[yy][xx] == '.') { visit_[yy][xx] = true; queue.push(XY(xx, yy)); } } } } }
座標値はintにパックするようにしました。パックには以下のマクロを用いています。与えられる迷路のサイズが最大55であるということで、55以上の一番小さなの2の累乗の数(2nの数。2、4、8、16、...等)、64を選びました。これにより、ビットシフトやビットマスクを用いて座標値のパックやアンパックをすることができます。
#define X(x) ((x) & 63) // Unpacking #define Y(x) ((x) >> 6) #define XY(x, y) (((y) << 6) + (x)) // Packing
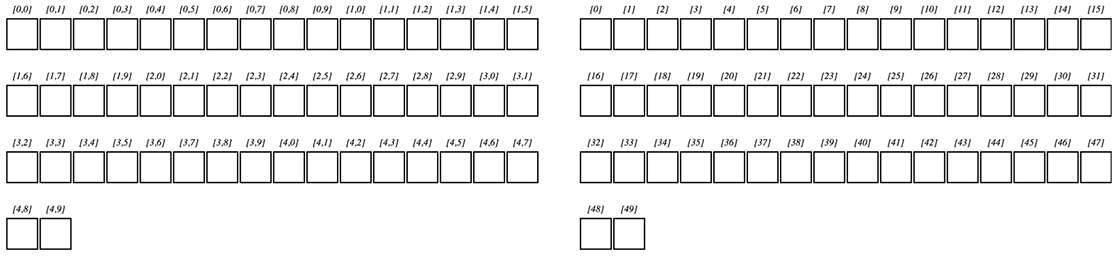
下位16ビットの使い方は以下のようになっています。
また、dx、dyには上左下右の位置に対応する差分値が格納されています。SRMでもよく見る典型的な手法です。
const int dy[] = {-1, 0, 1, 0}; const int dx[] = { 0, -1, 0, 1};
ここで、この実装のベンチマークを取ってみましょう。initメソッド経由で55 × 55の盤面を与え、3秒の間にどれだけbfsメソッドを呼べるかを計測してみました。私の端末では111,410回呼び出すことができました(OS X 10.9.5 + clang + -O2フラグを使用)。
さて、TopCoderのマラソンマッチではアルゴリズムの善し悪しが勝負を決めます。これは決定的で揺るぎない事実です。そのため、闇雲に高速化を行うことは一般的に悪手とされています。しかし、思いついたアルゴリズムがトップ争いを征するポテンシャルを備えていたとしても、アルゴリズムを計算する速度が遅いと勝つことができません。これは勿体ない。
例えばここで説明をしている単純な幅優先探索等はその動作が速ければ速いほど有利になるかもしれません。少しばかり時間をかけ、チューンアップすることを考えてみましょう。
まずSTLのパフォーマンスを疑ってみましょう。盤面をCの二次元配列で持つように直してみます。メンバ変数の宣言と初期化部分の実装を変更するだけですので、変更箇所は少ないです。
class solver_t { private: char a_[64][64]; int N_; bool visit_[64][64]; };
void solver_t::init(const std::vector<std::string>& a) { N_ = a.size(); for (int i = 0; i < N_; i ++) for (int j = 0; j < N_; j ++) a_[i][j] = a[i][j]; }
二次元配列に置き換える際に考慮すべきこととして、各要素の要素数が上げられます。座標値をパックした際と同様に、まず2の累乗の数を検討してみるのがよいでしょう。ここでも55以上の一番小さな2の累乗の数、つまり64を選択しました。
たったこれだけの変更ですがbfsを呼び出す回数は164,900回に増えました。約1.5倍の速度改善です。STLのコンテナは大変便利ですが、処理速度を重視する必要がある場合、Cの原始的な配列に置き換えることを検討するのは良手の一つです。
ではこの実装をさらに速度改善する方法を考えてみます。一次元配列に直してみましょう。メンバ変数は以下のようになります。盤面を表すa_メンバ変数だけではなく、visit_メンバ変数にも一次元配列を採用していることに注意してください。
class solver_t { private: int N_; int LASTROW_; char a_[4096]; // 64 * 64 = 4096 bool visit_[4096]; };
LASTROW_は大変便利な変数です。盤面の範囲をチェックする際に用います。これに関しては後ほど説明をします。
盤面の初期化は以下のようになります。
void solver_t::init(const std::vector<std::string>& a) { N_ = a.size(); LASTROW_ = (N_ - 1) << 6; for (int i = 0, p = 0; i < N_; i ++, p += 64) for (int j = 0, pp = p; j < N_; j ++, pp ++) a_[pp] = a[i][j]; };
また、bfsの実装は以下のようになります。
void solver_t::bfs(int sx, int sy, int ex, int ey) { memset(visit_, 0, sizeof(visit_)); int s = XY(sx, sy), e = XY(ex, ey); std::queue<int> queue; queue.push(s); visit_[s] = true; while (! queue.empty()) { int p = queue.front(), pp; queue.pop(); int x = X(p); if (p >= 64 && ! visit_[pp = p - 64] && a_[pp] == '.') { if (pp == e) return; visit_[pp] = true; queue.push(pp); } if (x > 0 && ! visit_[pp = p - 1] && a_[pp] == '.') { if (pp == e) return; visit_[pp] = true; queue.push(pp); } if (p < LASTROW_ && ! visit_[pp = p + 64] && a_[pp] == '.') { if (pp == e) return; visit_[pp] = true; queue.push(pp); } if (x < N_ - 1 && ! visit_[pp = p + 1] && a_[pp] == '.') { if (pp == e) return; visit_[pp] = true; queue.push(pp); } } }
何かすごいことになってしまった感もありますが、これまでと同様に3秒間の呼び出し回数を計測してみると282,420回となりました。Cの二次元配列を用いていたときから2倍弱の速度改善で、STLに比べると3倍弱の速度改善、といったところでしょうか。
何故このような速度改善が達成できるかは後ほど考えてみるとして、まず実装を見て行きましょう。whileによる反復部分です。pはキューから取得した現在の位置です。この値はx座標値とy座標値をintにパックしたものでした。
ここから、以下の処理を上左下右のそれぞれの方向に対して適用しています。
- 次の位置に進めるかを判定し、
- ppに次の位置を保持しつつすでに訪れているか否かを判定し、
- 次の位置が壁でなければ、
- 目的の位置であれば、探索を終了する
- 目的の位置でなければ、次の位置をキューに積む。この際、次の頂点に訪れることを記録する
「キューに積む際に次の頂点に訪れることを記録する」のはとても大事なので特に注意しましょう。これにより、同じ頂点が再びキューに積まれることを抑制することができます。
さて、位置pから上の方向に訪れることができるかどうかは、位置pが2行目以降にあればよいことになります。これは、pと64を比較すれば判定できます。
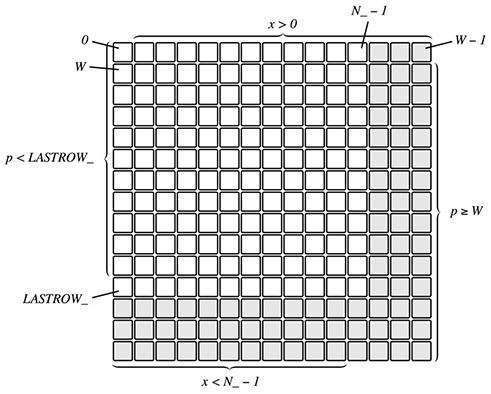
では位置pから下の方向に訪れることができるかどうかはどのように判定すればよいでしょうか? 予め計算しておいたLASTROW_をここに用います。LASTROW_はこのように計算していますので、
LASTROW_ = (N_ - 1) << 6;
以下の図に示す位置を表すことになります。そのため、現在の位置pがLASTROW_より小さければ、下方向に探索を進めても盤面からはみ出ないことが保証されるのです。
余談ですが、この変数の使い方はTopCoderマラソンマッチでは必ず上位に食い込んでいるwleiteさんの実装を眺めていて見つけました。とてもスマートな方法ですよね。
水平方向に関しては現在のx座標値をデコードしたほうが判定がしやすいのでそのようにします。これをまとめると以下となります。
さて、何故このような速度改善が達成できたのでしょう? メモリ構造が異なるのでしょうか? いえ、Cの二次元配列と一次元配列は何れも連続して確保されるはずです。例えば、char a[5][10]として配列を確保した場合とchar a[50]として配列を確保した場合、アドレッシングの差はあれど、メモリの確保のされかたは等しくなるはずです(大きな図で見たい場合は画像をクリックしてください)。
そのため、アドレッシングをする際にかけ算かビットシフトが入ることが性能低下の原因であると考えるのが自然です。
ここで少しだけアセンブラを眺めてみましょう。64 × 64の二次元グリッドにランダムに数値を設定し、ランダムにピックアップした頂点の値のxorを取る関数を書いてみます。繰り返し数は10000回です。
int rand64(); // ランダムに[0, 64)を返す関数が外部定義してあるものとする int rand4096(); // ランダムに[0, 4096)を返す関数が外部定義してあるものとする static int a[64][64]; int test_a() { int x = 0; for (int i = 0; i < 10000; i ++) x ^= a[rand64()][rand64()]; return x; } int test_b() { int* p = reinterpret_cast<int*>(&a[0][0]); int x = 0; for (int i = 0; i < 10000; i ++) x ^= p[rand4096()]; return x; }
二次元配列を使ったtest_a関数のアセンブラ(の主要な部分)は以下のようになります。
xorl %r15d, %r15d # %r15dレジスタを0にする movl $10000, %ebx # %ebxレジスタを10000にする leaq __ZL1a(%rip), %r12 # 二次元配列aの先頭のアドレスを%r12レジスタに格納する LBB1_1: callq __Z2rand64v # rand64関数をコールする movl %eax, %r14d # 結果を%r14dレジスタに格納し、 andl $63, %r14d # 63とandを取る(これがxとなる) callq __Z2rand64v # rand64関数をコールする andl $63, %eax # 63とandを取る(これがyとなる) shlq $8, %rax # yを8ビットシフトする # (intが4バイト長であるため、6 + 2ビットシフトしている) addq %r12, %rax # aの先頭のアドレスを足す xorl (%rax,%r14,4), %r15d # さらに、xの4倍分を足したアドレスの値とxorを取る decl %ebx # %ebxレジスタから1を引く jne LBB1_1 # %ebxが0でなければ反復する
これに比べ、一次元配列を使ったtest_b関数のアセンブラは以下のようになります。反復の内側で実行されるニモーニックの数がとても少ないことが分かります。
xorl %r14d, %r14d # %r14dレジスタを0にする movl $10000, %ebx # %ebxレジスタを10000にする leaq __ZL1b(%rip), %r15 # 二次元配列aの先頭のアドレスを%r15レジスタに格納する LBB2_1: callq __Z2rand4096v # rand4096関数をコールする andl $4095, %eax # 4095とandを取る(これをpとする) xorl (%r15,%rax,4), %r14d # b + p × 4のアドレスの値とxorを取る decl %ebx # %ebxレジスタから1を引く jne LBB2_1 # %ebxが0でなければ反復する
たとえ二次元配列を2の累乗の数で確保していたとしても、アドレッシングの計算の際にビットシフトと加算、また多少のレジスタのコピー操作が入ってしまうのです。たったこれだけなのですが、速度的には相当分が悪いのです。
キュー
さて、さらなる速度改善を考えてみましょう。具体的にはstd::queueもより原始的なデータで置き換えられないでしょうか?
キューの先頭と末尾の位置を保持するインデックスを2つ用意すると、一次元配列でキューを作成することができます。例えばアルゴリズムCに掲載されているキューの実装は以下のようにとてもシンプルです。
#define max 100 static int queue[max+1],head,tail; put(int v) { queue[tail++] = v; if (tail > max) tail = 0; } int get() { int t = queue[head++]; if (head > max) head = 0; return t; } queueinit() { head = 0; tail = 0; } int queueempty() { return head == tail; }
このデータ構造はstd::queueと比べ、ずっとずっと原始的です。例えば、キューに溜めるべき要素の数がmax個を超えた場合、プログラムは破綻します。そのため、キューに溜まる最大の要素の数を予め考察しておくことが大切なのですが、なかなか難しく、テストを繰り返しながらパラメータを調整する手法に頼りがちです。
問題によっては発想を少し変えることによってキューの実装がより簡単で安全なものになります。今回の迷路の最短経路探索にて使用している幅優先探索はそのような問題の一つです。
幅優先探索が訪れる最大の頂点数がどのくらいか考えてみましょう。すでに訪れている頂点にはもう訪れることがないことを考えると高々N2です(Nは頂点数ではなく、迷路の幅であることを思い出してください)。そのため、要素数がN2の一次元配列を確保しておけばどのような状況であってもキューがはみ出さないことが分かります。ここではアライメントを考慮して、642分の要素を確保することにします。さらに、putやget関数を以下のように簡略化することができます。
#define max 4096 static int queue[max],head,tail; put(int v) { queue[tail++] = v; } int get() { return queue[head++]; }
if文と代入を取り除いているだけですが、速度に大きく影響することにも注意してください(自分の端末だと、10%ほど速度に影響を与えました)。
さて、では実装を見てみましょう。メンバ変数としてqueue_を用意します。
class solver_t { private: int N_; int LASTROW_; char a_[4096]; bool visit_[4096]; int queue_[4096]; };
bfsの実装は以下のようになります。
void solver_t::bfs(int sx, int sy, int ex, int ey) { memset(visit_, 0, sizeof(visit_)); int s = XY(sx, sy), e = XY(ex, ey); visit_[s] = true; int q1 = 0, q2 = 0; queue_[q1 ++] = s; while (q1 != q2) { int p = queue_[q2 ++], pp; int x = X(p); if (p >= 64 && ! visit_[pp = p - 64] && a_[pp] == '.') { if (pp == e) return; visit_[queue_[q1 ++] = pp] = true; } if (x > 0 && ! visit_[pp = p - 1] && a_[pp] == '.') { if (pp == e) return; visit_[queue_[q1 ++] = pp] = true; } if (p < LASTROW_ && ! visit_[pp = p + 64] && a_[pp] == '.') { if (pp == e) return; visit_[queue_[q1 ++] = pp] = true; } if (x < N_ - 1 && ! visit_[pp = p + 1] && a_[pp] == '.') { if (pp == e) return; visit_[queue_[q1 ++] = pp] = true; } } };
これまでと同様に3秒間の呼び出し回数を計測してみましょう。結果、373,280回となりました。初めに比べると3.5倍以上の速度改善を達成したことになります。
経路復元
さて、次は機能拡張をしてみましょう。bfsメソッドが幅優先探索によって発見した最短経路を返すように変更します。つまり、経路復元を行います(経路復元については@machyさんが去年のアドベントカレンダーで記載したスライドが大変秀逸ですのでご一読することをお勧めいたします)。
経路復元は以下のように行います。
- 「その頂点にはどの頂点から訪れたか?」という情報を別途記録しておく
- 終点を発見したら、始点までさかのぼる
「その頂点にはどの頂点から訪れたか?」という情報は相対位置情報(上から来た、下から来た等)でも構いませんが、ここでは絶対位置情報を記録することにします。
探索が終わったときの経路情報は以下のようなものとなります。見方を変えると、これは始点を根とした木であるとも言えます(薄く描画されている辺は、終点が発見されたことにより探索が打ち切られ、調べられなかった辺を表しています)。
さて、メンバ変数を追加しましょう。木を意識して、parent_という変数名を選択しました。
class solver_t { private: int N_; int LASTROW_; char a_[4096]; bool visit_[4096]; int queue_[4096]; int parent_[4096]; };
bfsの実装は以下のようになります。0はパックされた座標として有効ですので、-1で根を表すことにしました。また、探索を行う毎にparent_の内容を全て初期化する必要がないことに注意しましょう。探索と共に経路情報が木のように育っていることを意識すると分かりやすいかもしれません。
std::vector<int> solver_t::bfs(int sx, int sy, int ex, int ey) { memset(visit_, 0, sizeof(visit_)); visit_[XY(sx, sy)] = true; parent_[XY(sx, sy)] = -1; int e = XY(ex, ey); int q1 = 0, q2 = 0; queue_[q1 ++] = XY(sx, sy); while (q1 != q2) { int p = queue_[q2 ++], pp; int x = X(p); if (p >= 64 && ! visit_[pp = p - 64] && a_[pp] == '.') { parent_[pp] = p; if (pp == e) break; visit_[queue_[q1 ++] = pp] = true; } if (x > 0 && ! visit_[pp = p - 1] && a_[pp] == '.') { parent_[pp] = p; if (pp == e) break; visit_[queue_[q1 ++] = pp] = true; } if (p < LASTROW_ && ! visit_[pp = p + 64] && a_[pp] == '.') { parent_[pp] = p; if (pp == e) break; visit_[queue_[q1 ++] = pp] = true; } if (x < N_ - 1 && ! visit_[pp = p + 1] && a_[pp] == '.') { parent_[pp] = p; if (pp == e) break; visit_[queue_[q1 ++] = pp] = true; } } std::vector<int> path; for (int p = e; p != -1; p = parent_[p]) path.push_back(p); std::reverse(std::begin(path), std::end(path)); return path; };
さて、今回は絶対位置情報を使いましたが、何れのデータ構造が得であるかは問題と場合に依ります。相対位置情報で記録したほうが省メモリかもしれません。ですが、経路復元をする際に座標値の再計算が必要となるかもしれません。また、絶対位置情報では再計算を行わないかもしれませんが、相対的な方向を解として保持しなけらばならない場合、やはり再計算が必要となるかもしれません。
コスト付き最短経路探索
最後にコスト付き最短経路探索を考えてみましょう。頂点のコストを加味した最短経路探索はこれまで扱ってきたコストを考えない最短経路探索よりもずっと複雑ですが、より現実的な問題設定であると言えると思います。
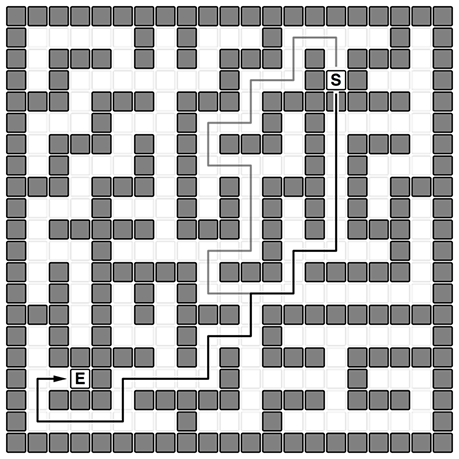
ここでもこれまでに扱ってきた迷路のデータを使用しましょう。これまで壁は通れないものとして扱ってきましたが、通り抜けられるようにしてしまいましょう。そして、以下のようにコストを設定してみましょう。
- 通路を一つ進む度にコストが1かかる
- 壁を一つ乗り越える度にコストが10かかる
この条件下では壁を一つ乗り越えることで、10個以上の通路をスキップしてしまったほうがよい状況を考えなければいけなくなります。例えば、以下の例では始点のすぐ下で一回壁を乗り越えたほうが得であるようです(参考として、壁を乗り越えない場合の最短経路を薄い色の経路で表しています)。
随分と実際のマラソンマッチの様相を呈してきました。事実、この問題設定は冒頭で紹介したMM82のものにとても類似しています。
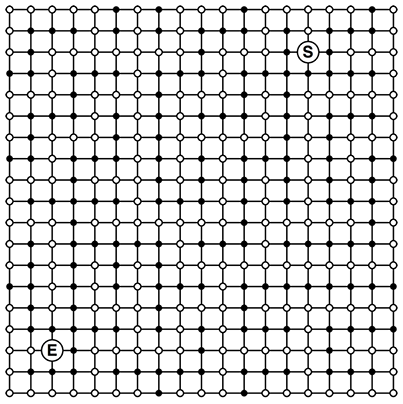
先ほども触れましたが、この問題設定はなかなか複雑で難しいものです。前半でやったのと同様に、迷路をグラフとして表現してみましょう。以下のような疎ではありますが、先ほどまでと比べるととても密度の高いグラフとなります(白い頂点は通路を表し、黒い頂点は壁を表しています)。
さて、この最短経路探索はどのようなアルゴリズムを用いるのが適切でしょうか? アルゴリズムに詳しいかたは迷いなくダイクストラ法を選択するでしょう。
二次元配列を使った実装から見て行くことにしましょう。優先度付きキューを伴ったダイクストラ法の実装は計算量を抑えることが知られています。std::priority_queueを使いましょう。コストが低い頂点から優先して処理を行うため、std::greaterを併用していることに気を付けてください。
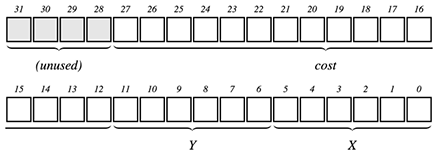
コストの上限は64 × 64 × 10として40960ですので、16ビット用意すれば大丈夫そうです。また、コストは初期化時に12ビット左にシフトしてしまうことにしました。位置情報と共にパックする際の実装が簡潔になるからです。そのため、パック、アンパックをするためのマクロも改変します。
#define X(x) ( (x) & 63) #define Y(x) (((x) >> 6) & 63) #define Z(x) ( (x) & -4096) #define P(x) ( (x) & 4095) #define XY(x, y) (((y) << 6) + (x)) #define PZ(p, z) ((z) + (p)) #define XYZ(x, y, z) PZ(XY((x), (y)), (z))
ビットの使い方は以下のようになりました。
では実装を見て行きましょう。a_にはもはや文字を収めません。12ビット分左にシフトしたコストを記録します。そのため、char型の配列ではなく、int型の配列として確保します。
class solver_t { private: int a_[64][64]; int N_; int cost_[64][64]; };
迷路のデータを受け取り次第、12ビット分左にシフトします。
void solver_t::init(const std::vector<std::string>& a) { N_ = a.size(); for (int i = 0; i < N_; i ++) for (int j = 0; j < N_; j ++) a_[i][j] = (a[i][j] == '.' ? 1 : 10) << 12; };
実装は以下のようになります。
int solver_t::dijkstra(int sx, int sy, int ex, int ey) { for (int i = 0; i < N_; i ++) for (int j = 0; j < N_; j ++) cost_[i][j] = INF; std::priority_queue<long long, std::vector<long long>, std::greater<long long>> pq; pq.push(XYZ(sx, sy, cost_[sy][sx] = a_[sy][sx])); while (! pq.empty()) { int x = X(pq.top()); int y = Y(pq.top()); int z = Z(pq.top()); pq.pop(); if (cost_[y][x] < z) continue; for (int k = 0; k < 4; k ++) { int xx = x + dx[k], yy = y + dy[k]; if (0 <= xx && xx < N_ && 0 <= yy && yy < N_) { int zz = z + a_[yy][xx]; if (xx == ex && yy == ey) return zz; if (zz < cost_[yy][xx]) { cost_[yy][xx] = zz; pq.push(XYZ(xx, yy, zz)); } } } } return -1; };
3秒間の計測を行います。39,490回でした(参考までに、STLを使った場合の実装は30,900回でした)。
さて、こちらを一次元配列を使って書き直してみましょう。std::priority_queueはそのまま使用します。
class solver_t { private: int a_[4096]; int N_; int LASTROW_; int cost_[4096]; };
int solver_t::dijkstra(int sx, int sy, int ex, int ey) { for (int i = 0, p = 0; i < N_; i ++, p += 64) for (int j = 0, pp = p; j < N_; j ++, pp ++) cost_[pp] = INF; int s = XY(sx, sy), e = XY(ex, ey); std::priority_queue<int, std::vector<int>, std::greater<int>> pq; pq.push(PZ(s, cost_[s] = a_[s])); while (! pq.empty()) { int x = X(pq.top()); int p = P(pq.top()), pp; int z = Z(pq.top()), zz; pq.pop(); if (cost_[p] < z) continue; if (p >= 64) { pp = p - 64; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { return zz; } else { pq.push(PZ(pp, cost_[pp] = zz)); } } } if (x > 0) { pp = p - 1; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { return zz; } else { pq.push(PZ(pp, cost_[pp] = zz)); } } } if (p < LASTROW_) { pp = p + 64; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { return zz; } else { pq.push(PZ(pp, cost_[pp] = zz)); } } } if (x < N_ - 1) { pp = p + 1; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { return zz; } else { pq.push(PZ(pp, cost_[pp] = zz)); } } } } return -1; };
一次元配列を用いた場合、dijkstraメソッドは45,840回呼び出すことができました。STLを用いたものに比べ、1.5倍高速です。
さて、ここまで来ると優先順位付きキューを一次元配列を利用できないのかな? と考えてしまいますね。しかし、優先順位付きキューは単純なキューのように機械的に一次元配列等に変換することはできません。残念。
ここで、優先順位付きキューの代わりに単純なキューを使うと何が起こるか考えてみましょう。この問題では負のコストがないため、優先順位付きキューを使えば最もコストが少ない頂点から訪れることが保証されていました。しかし、単純なキューを使った場合、例えば終点に初めて訪れた際のコストが最小である保証はなされません。
ならば、キューが空になるまで繰り返し、それぞれの頂点に訪れたコストの中で最小のものを記録するようにしてみましょう。言い換えれば、一つ前の頂点からの緩和を繰り返す、ということになります。何かどこかで見たことがありますね...? そうです、これはキューを伴ったベルマンフォードアルゴリズムです。
int bellman_ford(int sx, int sy, int ex, int ey) { for (int i = 0, p = 0; i < N_; i ++, p += 64) for (int j = 0, pp = p; j < N_; j ++, pp ++) cost_[pp] = INF; int s = XY(sx, sy), e = XY(ex, ey); int q1 = 0, q2 = 0; queue_[q1 ++] = PZ(s, cost_[s] = a_[s]); int zm = INF; while (q1 != q2) { int q = queue_[q2 ++]; int x = X(q); int p = P(q), pp; int z = Z(q), zz; if (cost_[p] < z || z > zm) continue; if (p >= 64) { pp = p - 64; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { zm = std::min(cost_[pp] = zz, zm); } else { queue_[q1 ++] = PZ(pp, cost_[pp] = zz); } } } if (x > 0) { pp = p - 1; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { zm = std::min(cost_[pp] = zz, zm); } else { queue_[q1 ++] = PZ(pp, cost_[pp] = zz); } } } if (p < LASTROW_) { pp = p + 64; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { zm = std::min(cost_[pp] = zz, zm); } else { queue_[q1 ++] = PZ(pp, cost_[pp] = zz); } } } if (x < N_ - 1) { pp = p + 1; if ((zz = z + a_[pp]) < cost_[pp]) { if (pp == e) { zm = std::min(cost_[pp] = zz, zm); } else { queue_[q1 ++] = PZ(pp, cost_[pp] = zz); } } } } return zm; };
実装部分はまあこれでよいとして、とても注意すべきことがあります。もはやキューの最大要素数はN2ではありません。緩和が終わるまでそれぞれの頂点に複数回訪れることを考えると不思議ではありません。
この問題でデータのアライメントを64と設定した場合、4,096の16倍、65,536個分を用意する必要がありました。理論的に計算できればカッコいいのですが、私はこれを実験的に決定しました。実際には50,000個ほどでも十分だと思います。
int queue_[65536];
優先順位付きキューを伴ったダイクストラ法では45,840回の探索でしたが、一次元配列によるキューを伴ったベルマンフォード法では59,600回の探索を行うことが出来ました。ほぼ1.3倍の速度改善です。STLを使ったものに比べると約2倍のパフォーマンス改善を行ったことになります。
この実装のポイントとして、以下の3種類の枝刈りを行っていることに触れておきましょう。
- 注目する頂点により低いコストで到達する経路がある場合
- 注目する頂点にたどり着いたコストが、現在までに見つかっている終点までのコストよりも大きい場合
- 隣接する次の候補の頂点により低いコストで到達する経路がある場合
2番目の枝刈りの条件は忘れやすいと思いますが(「z > zm」の条件)、特に重要です。これを忘れると、ダイクストラ法のパフォーマンスに遥かに及びません。
「ベルマンフォード法の計算量はダイクストラ法と比べ随分大きいんじゃないのか? 遅くなるんじゃないのか?」と考えたかたも多いのではないのでしょうか? 確かにその通りで、ベルマンフォード法を適用できるか否かは問題の性質に大きく依存します。例えば大部分が同じ設定であったとしても、盤面の大きさが999 × 999である場合は以下のことが起こります。
- キューの要素数を相当大きく確保しておく必要がある(例えば、67,108,864要素(= 1024 × 1024 × 64))
- 優先順位付きキューを伴ったダイクストラ法と比べ、半分以下の速度となってしまう。
最後に、この条件下での経路復元について簡単に触れておきます。キューを伴ったベルマンフォード法の場合も幅優先探索と変わらず、「その頂点にはどの頂点から訪れたか?」という情報を記録すれば十分に経路復元をすることが可能です。
こちらの問題設定では先ほどと比べ、多少複雑なグラフを扱うことになります(以下の図は再掲)。
しかし経路の情報は、やはり始点を根とした木の様相を成します。以下の図をよく見ると、薄い辺があります。これらの辺は緩和の課程で一度は接続されたものの他の最短な経路によって切断された辺です。ベルマンフォード法では同じ頂点に何度も訪れるため、親の頂点情報も何度も入れ替わるのです。
まとめ(または、回顧録)
今回はマラソンマッチにおける典型データ構造とアプローチという題材で多少のトピックを解説しました。それぞれのトピックを見直すと、以下の共通点があることが挙げられます。
- 原始的なデータ構造およびロジックは速い
- 二次元配列は意外に遅い
- 一次元配列は十分に単純であるため、速い
- メモリを動的に確保するのは遅い
- 問題に適したミニマムかつ効率的な設計を行う
「ひゃー、マラソンマッチではこんなに雑多な実装を行わなきゃいけないのか。つまらないじゃないか」と思われた方もいらっしゃるかもしれません。再掲となりますが、マラソンマッチで真に大切なのは問題にフィットしたロジックであり、アルゴリズムです。このエントリに記載されていることはある意味「おまけ」なのですが、トップ陣はそのおまけの部分も異様に強い。まるで魔術師を見ているようです。しかし、一つ一つのテクニックを丁寧に観察しひも解くと、実装の大部分に明確な理屈があり、ここで記載したような小さな工夫やチューニングが巧みに全体を構成しているのが見えてきます。このエントリがそんな「面倒臭い部分」に向き合うときの少しばかりの助けになれば大変嬉しく思います。
さて、この記事はCompetitive Programming Advent Calendar 2014 - PARTAKEのマラソン部門、12月6日分のエントリとして記載しました。これまでも、またこれからも続々とマラソンに関する記事が執筆されます。大変貴重なイベントだと思います。
アドベントカレンダーが始まってから実力者のエントリが続き、「問題をどう解くか」という核心の部分を熱く熱く執筆くださっています。素晴らしい記事を読むにつれ、自分の選んだ題材はあまりにも稚拙だよなあ? と迷いながらも、特に日本のマラソンマッチコンペティターの底上げに少しでも貢献できればと思い、なんとか書き上げました。
さて、そもそも今年の競技プログラミングアドベントカレンダーにマラソン部門が出来たことに関して少し触れておきたいと思います。私が日本に一時帰国した際にhotpepsiさんが開催してくださった飲み会の席でのことでした。突然、simezi_tanが熱く、そして激しく、「マラソンは何をしていいか分からない。競技プログラミングのアドベントカレンダーにマラソン部門が欲しい!」と声を上げたのです。tomerunさんやmachyさん達の援護が加わったこと、また、_tanzaku_さんが柔軟な企画、そして対応をしてくださったこともあり、気がついたときには見たこともない素晴らしいイベントとして運用されることになっていました。日本の競技プログラミングコミュニティの柔軟さには舌を巻くばかりです。
そんなsimezi_tanに伝えたいことがあります。この場を借りて記したいと思います。
「おいしめたん。そもそもの言い出しっぺなんだから参加しなはれ(何が分からないか書いてみるとか)」
明日、12月7日はyowaさんが「マラソンマッチで1位になる方法（最終順位とは言ってない）」という題材で執筆なさる予定です。お楽しみに。
Precalculating a Combination
異なるn個のものから異なるk個のものを選ぶ組み合わせは以下のように計算することができます。
階乗を使うとより簡潔に書くことができます。
とてもシンプルに見えますよね。しかし、計算機で組み合わせの計算を行うのは意外と厄介なのです。階乗はとても大きな値になるからです。例えば、32!は以下のような結果になります(決して大きいとは言えない32個の数字を掛けただけなのに!)。
unsigned long longで表すことのできる数値の限界が18446744073709551615、つまり1.8e+19ほどであるのに比べ、32!は8.2e+33です。多倍長整数をサポートしない処理系で、例えば32C16を階乗を用いて計算するのはとても難しいのです。
さて、nCkは漸化式を用いても計算することができます。
漸化式を使えば階乗を使う必要がありません。また漸化式を眺めると和算しか使っていないことが分かります。そのため、計算の途中に結果より大きな値に出くわすことがない、と考えることができます。
そのため、漸化式の特徴を考慮して、ある程度の組み合わせの数を予め二次元配列に計算しておく手法がよく使われています。
nck = [[0] * 111 for i in range(111)] nck[0][0] = 1 for i in range(1, 100 + 1): nck[i][0] = nck[i][i] = 1 for j in range(1, i): nck[i][j] = nck[i-1][j-1] + nck[i-1][j]
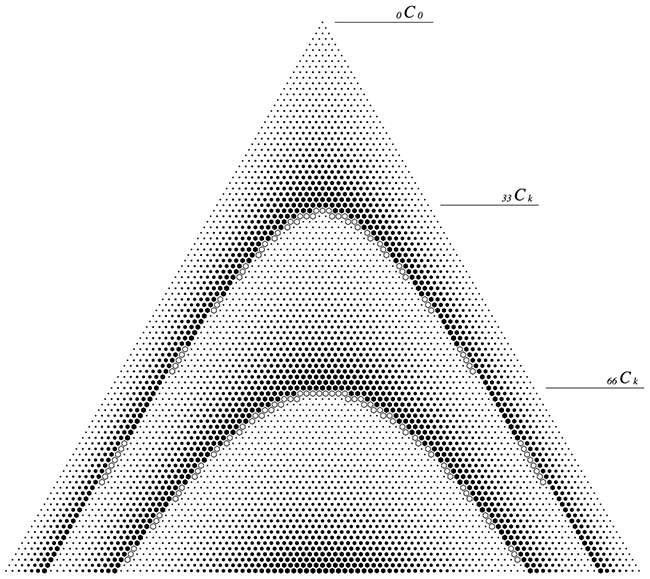
Pythonは多倍長整数が扱えるため、オーバーフローを考えずに100Ckまでの値を計算させてしまいました。しかし、C++等では選んだ整数の型によって比較的すぐオーバーフローしてしまうはずです。この限界をしっかり把握するため検証を行い、結果を図にしてみました。
組み合わせの数を三角形状に並べたものはパスカルの三角形として知られています。パスカルの三角形の最初の10段は以下のようになっています。先の図には数値が記載されていませんが、同じように並べていると考えてください。
結果、int型は0 ≦ n ≦ 33までのnCkが、また、long longでは0 ≦ n ≦ 66までのnCkが扱えることが分かりました。
また、nはそれぞれの型のビット数に近い値であることも分かりました。漸化式からnCkの最大値はn-1Ckの最大値の高々2倍の大きさにしかならないことが分かるので、まあ納得です。
まとめ
組み合わせの数を扱う場合はこの限界値を元に、効率的に考察を行うことが出来そうです。
- nが33までのnCkはintの二次元配列で予め計算しておくことができる
- nが66までのnCkはlong longの二次元配列で予め計算しておくことができる
計算式によっては、漸化式を用いずに階乗を約分して算出したほうが有利な場合もあるでしょう。また、誤差の許容量によっては対数空間での計算や、また、lgamma関数を使うことを検討してもよいでしょう。
何れにせよ組み合わせの数を用いた計算は実装時に大きな数の扱いで困ってしまうことが多いので、適切な戦略を立ててから実装を始めることが肝心なようです。
組み合わせの数を二次元配列で予め計算しておく方法は正直苦手意識を感じていました。ですが今回の考察で少し自信を持って考えることが出来るようになったと思います。
Past, Present and Future
Past, Present and Future
コンテスト中に自分のブログから該当するエントリを探す作業をよくしていることに気付いたので、インデックスを作成しておくことにした。
Google Code Jam 2012 Round 1A
- Kingdom Rush
- std::sort()のコンパレータオブジェクトについて考察
Understanding How std::string::substr works
- Understanding How std::string::substr works
- std::string::substr()について考察
Recalling Bayes' Theorem
定理を素早く思い出したりするために自分にとっての「定型」の問題を用意しておくことがままあります。
例えばベイズの定理の場合。「囚人問題」や「モンティホール問題」が特に有名なので、それを「定型」としている方もいらっしゃるのではないでしょうか。
私が「定型」としている問題の一つは道具としてのベイズ統計に掲載されていた以下の問題です(第2章 3. 壷の問題を考える。p. 51)。
二つの壷a、bがある。壷aには赤玉が3個、白玉が2個入っている。壷bには赤玉が8個、白玉が4個入っている。壷aと壷bが選ばれる割合は1:2とする。どちらかの壷から玉1個を取り出したとき、それが赤玉であった。その赤玉が壷aから選ばれている確率を求めよ。
道具としてのベイズ統計
「壷aと壷bが選ばれる割合は1:2とする」の一節はどのように解釈するものなのだろう...? などと疑問に思い続けてはいますが、まあ壷は目の届かない場所にでも置いてあるんだろうななどとといいように解釈しつつ、長年付き合っています。
さて、壷aを選ぶ事象をA、どちらかの壷から玉1個を取り出したときにそれが赤玉である事象をRとします。問題が求めているのは、「どちらかの壷から玉1個を取り出したとき、それが赤玉であった。その赤玉が壷aから選ばれている確率」です。これは条件付き確率Pr(A | R)となります。
さて、ここでベイズの定理を書き出してみましょう。
同時確率Pr(A, R)は条件付き確率Pr(A | R)と周辺確率Pr(R)の積として計算できるのでした。同様に、同時確率Pr(R, A)は条件付き確率Pr(R | A)と周辺確率Pr(A)の積として計算できるのでした。
同時確率Pr(A, R)とPr(R, A)は等しいので、以下の等式が成り立ちます。
両辺をPr(R)で割って、
ベイズの定理を導くことができました。ここまでは簡単ですね。では、それぞれの確率に値を入れて計算してみましょう。
...うん、ここで少し立ち止まってみましょう。単純に確率の値を入れる前に、それぞれの確率がベイズの定理ではどのように呼ばれるかを復習しておきます。そのほうが効率的です。
左辺Pr(A | R)は求める確率です。
式を見れば一目瞭然、条件付き確率です。「どちらかの壷から玉1個を取り出したら赤玉であった」ときに「選んだ壷が壷aであった」確率です。ベイズの定理ではこれを事後確率(Posterior Probability)と呼びます。
右辺Pr(A)は「壷aが選ばれる」確率です。
ベイズの定理ではこれを事前確率(Prior Probability)と呼びます。右辺の中では一番重要です。壷の中がどのような状態になっているか知らなくても、その選ばれ方に関して何かしら事前に知っている情報だからです(どうです、重要そうでしょう?)。
右辺Pr(R | A)も条件付き確率です。
ベイズの定理ではこれを尤度(Likelihood。「ゆうど」と読みます)と呼びます。
この場合の尤度は、「壷aが選ばれた」ときに「取り出した玉が赤玉であることはどのくらいであるか」を示しますが、あまりこのように記載されることはありません。どちらかといえば、「壷aが選ばれた」ときに「取り出した玉が赤玉であることはどのくらいもっとも(尤も)らしいか」といったように記載されます。
最後に、右辺のPr(R)は規格化定数(Normalize Constant。証拠(Evidence)とも呼ばれます)などと呼ばれています。
この項はベイズの定理を考える上であまり活躍することはありません(これはベイズの定理を学んで行けば行くほどはっきりしてきます)。
さて、では実際に計算をしてみましょう。まずは事前確率Pr(A)です。「壷aと壷bが選ばれる割合は1:2」なのでした。そのため、壷aが選ばれるのは1 / 3ですね。
次に尤度Pr(R | A)を考えてみましょう。尤度は「壷aが選ばれた」ときに「取り出した玉が赤玉であることはどのくらいもっともらしいか」を示しているのでした。ちょっと何言っているかよく分かりませんよね。
こういうときは極端な例を考えてみるのも一つの手です。例えば、壷aの中には赤玉しか入っていないとしましょう。赤玉の数はなんでもよいです。流れに沿って赤玉が5個入っていると考えてもよいかもしれません。このとき、尤度はどうなるでしょう?
尤度は「壷aが選ばれた」ときに「取り出した玉が赤玉であることはどのくらいもっともらしいか」と考えるのでした。今は極端な例を考えているので、「壷aが選ばれる」と「取り出す玉は全て赤玉である!」と考えられます。先ほどの書き方をすれば、「壷aが選ばれた」ときに「取り出した玉が赤玉であることはたいへんもっともらしい」と考えておきましょう。
では壷aの中には白玉しか入っていない例を考えてみましょう。この場合の白玉の数もなんでもよいです。もちろん、白玉が5個は言っていると考えてもよいです。
先ほどと同様に考えると、「壷aが選ばれた」とき「取り出す玉は全て白玉である!」と考えられます。こちらは「壷aが選ばれた」ときに「取り出した玉が赤玉であることは全くもってもっともらしくない!」とでも考えられます。
どうでしょう、少し「もっともだ」という言い回しに慣れたでしょうか?
では元の例を考えましょう。「壷aには赤玉が3個、白玉が2個入っている」例です。
「壷aを選ばれた」ときに「取り出した玉が赤玉であることはどのくらいもっともらしいか」。5個のうち3個は赤玉ですから、「60%の確率でもっともらしい」と言うことができそうです。初めのうちはもっとカジュアルに、「赤玉を取り出すのは6割くらいでもっともらしいかな...」などと表現してもよいかもしれません。
さて、事前分布、尤度に関して考えました。後は規格化定数について考えれば計算できますね...ですがこのエントリではここでPr(B | R)について考えます。つまり、「どちらかの壷から玉1個を取り出したとき、それが赤玉であった。そのとき、その赤玉が壷bから選ばれている確率は如何ほどか」を考えます。もう少しお付き合いください。
Pr(B | R)はベイズの定理を用いて、以下のように計算できます。
AとBが入れ替わっただけです。簡単ですね。あまり重要視されていなかった分母に至っては変わりません。
事前分布Pr(B)や尤度Pr(R | B)も簡単に求めることができます。
事前分布も尤度も66.7%でした(これらが同じ値であることに意味はありません)。ここでまた例え話をしましょう。「壷aと壷bは同じ割合で選ばれる」としたらどうでしょう? 「どちらかの壷から玉1個を取り出したとき、それが赤玉であった」ら、「赤玉が出る尤度がより高い壷から取り出したのでは?」と考えるのがより自然ではないでしょうか? 尤度という概念を導入すると、何か人間の自然な思考で考えられるような気がしてきませんか。
もちろん尤度だけでは判断できません。例えば壷aが全て赤玉で詰まっていたとしても、つまり最高潮にもっともらしかったとしても、「壷aと壷bが選ばれる割合は1:100」であったら、壷aから玉自体が取り出される機会がそのものが大変少ないのです。
尤度と事前分布の積を取るのはそのためです。言い換えれば、「ところで全体からするとどの割合でもっともらしいの?」という問いの答えなんですね。ちょっと条件付き確率の考え方に似てますね。
では早速計算してみましょう。
積の値を比較してみたいですね。そのような場合は通分すればよいのでした。
その結果、9:20の割合であることが分かりました。
この割合は「どちらかの壷から玉1個を取り出したら赤玉であった」ときに「選んだ壷が壷aであったか壷bであったか」の割合でもあります。そのため、元の問題の答えもここから計算することができます。
少しトリッキーでしたが、規格化定数を使うことなしに事後確率、つまり「どちらかの壷から玉1個を取り出したら赤玉であった」ときに「その赤玉が壷aから選ばれている」確率を計算することができました。
どうやら事後確率は31%であるようです。事前確率、つまり「事前に情報がないときに壷を選んだら壷aである」確率が33.3%であったので、「どちらかの壷から玉1個を取り出したら赤玉であった」ことで確率が少し落ちたことになります。元々壷bから玉を取り出すことが多い上に、壷bのほうが少し尤度が高かったため、壷aから赤玉を取り出す確率が下がった、と考えるとよいでしょう。
まとめ
今回はベイズの定理について記載しました。
ほとんどの書籍は式を導いた後にすぐ具体的な例を解説していますが、自分にとっては
- どの項が「事後確率」「事前確率」「尤度」「規格化定数」を表しているか
- またその項の重要度はどうか
を頭に入れた後に読み進めたほうが理解が早かったように記憶しています。
どの分野を学ぶときもそうですが、自分の得意なパターンや例題を見つけるのは大事なように思います。理解できるなと思えるのは本当に嬉しいことですし、効率も上がるように思います。
- 作者: 涌井良幸
- 出版社/メーカー: 日本実業出版社
- 発売日: 2009/11/19
- メディア: 単行本
- 購入: 10人 クリック: 71回
- この商品を含むブログ (18件) を見る
- 作者: J.アルバート
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本（ソフトカバー）
- この商品を含むブログ (1件) を見る
