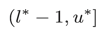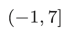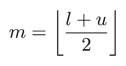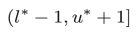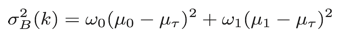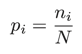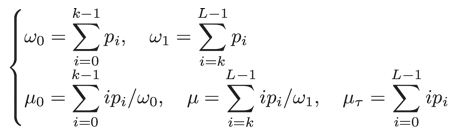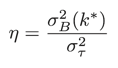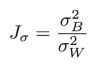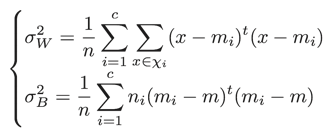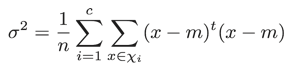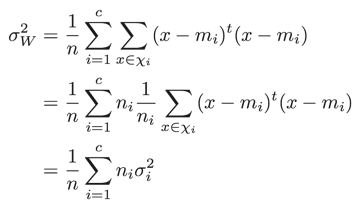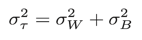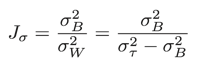Idiom: Calculating Power of 10 using pow Function in Integer Arithmetic

Algorithm !

今日参加したコンテストで有効な電話番号の組み合わせ数を求める問題が出題されました。実装ではlong longの大きな値、例えば\(10^{17}\)から小さな値、例えば10や1を引く演算を行う必要がありました。

powを使って10の冪乗を計算する解法も少なくなかったのですが、おそらくそのほとんどはテスト時に落ちてしまいました。どうやら計算誤差が原因のようです。

これは自分にとっても大きな驚きでした。xが整数である場合、pow(10, x)がきっちりと10の冪乗を返すことを知っていたからです。

  long long x = 1;
  
  for (int i = 0; i < 18; i ++, x *= 10)
    assert(pow(10, i) == x);            // pow(10, i)は問題なし

どこで計算誤差が出ているかを考えるために以下のような実装を用意しました。\(10^{17} - (10^0 + 10^1 + 10^2)\)を計算する実装です。期待している答えは末尾が...,999,889となるはずです。

long long c = pow(10, 17);

assert(c == 100000000000000000LL); // ここは問題なし

std::vector<int> a = {0, 1, 2};

for (const auto& i : a)
  c -= pow(10, i);

assert(c == 99999999999999889LL);  // ここでアサーションエラー!

変数cの内容をチェックしました。期待とは異なり、99,999,999,999,999,888でした。

さて、以下は期待通り...,999,889を返します。

long long c = pow(10, 17);

assert(c == 100000000000000000LL);      // ここは問題なし

astd::vector<int> a = {0, 1, 2};

for (const auto& i : a)
  c -= static_cast<long long>(pow(10, i));

assert(c == 99999999999999889LL);       // ここも問題なし!

どうも自分はこれまで、-=演算子は左側の変数の型で演算される、と思い込んでいたようです。つまり右辺の値がまずlong longにキャストされると考えていました。実際には二項の加減算演算子の振る舞いと同様に、doubleにキャストされてから計算され、改めてlong longにキャストされるようです。

これまで挙動を正確に把握していなかったこともあり、pow関数を使って10の冪乗を計算しないようにしていましたが、次のようなイディオムとして今後積極的に使っていきたいな、と考えています。またこの知見を大好きなハックにも役立てたいです。

long long y = static_cast<long long>(pow(10, x));

最後になりますが、TLで気さくに質問に答えてくださった@n_vipさん、ありがとうございました。

追記

これは実装依存の挙動だそうです。一般的に、pow(x, y)のyが整数のときはpowを使うべきではないとのこと。naoya_tさんにご指摘いただきました。どうもありがとうございます)。

参考: c++ - Definitions of sqrt, sin, cos, pow etc. in cmath - Stack Overflow

Series of Xor Arithmetics

Algorithm !

先日参加したコンテストにこんな問題が出題されました。排他的論理和を使う問題です。

nとxが与えられる。n個の異なる整数のビットごとに排他的論理和を取ってxとなるようにしたい。n個の非負整数を出力せよ

ただし、1 ≦ n ≦ 105、0 ≦ x ≦ 105とし、出力する非負整数は106までとする

排他的論理和は融通が効く印象がありました。n - 1個の0から始まる連続した整数を用意してそのビットごとの排他的論理和を取り、最後の一個で辻褄を合わせられるんじゃないか? と考えました(その方針の元で実装した解法は無事、システムテストを通過しました!)

排他的論理和の計算は色々なアルゴリズムに登場します。例えばZobrist HashingやRolling Hashを考えるとき、排他的論理和は欠かせません。今回のエントリでは連続した排他的論理和の計算方法について紹介したいと思います。

さて、{1, 0, 0, 1, 0, 1, 0, 1}という数列の排他的論理和を計算することを考えてみましょう。左から演算を行っていくと以下のように計算することができます。

f:id:agw:20171004051714p:plain

なかなか時間がかかりますね。工夫をしてもっと速く計算できるようにならないでしょうか? 排他的論理和の演算は順序を入れ替えても結果が変わりません。これは利用できないでしょうか?

f:id:agw:20171004051700p:plain

試しに、先ほどの数列の隣り合った数を入れ替えてみましょう。

f:id:agw:20171004051719p:plain

先ほどと同様、左から計算します。

f:id:agw:20171004051722p:plain

無事同じ結果になりました(まあ答えは0か1にしかならないので、あまり説得力がないようにも思えますが...)。

もっと入れ替えれば数列を整列できそうです。具体的には0の数字の集まりと1の数字の集まりにできそうです。

f:id:agw:20171004051728p:plain

さて、0と0の排他的論理和は0なのでした。つまり、0 xor 0 = 0。また、0 xor 0 xor 0は(0 xor 0) xor 0と計算すればいいので、0 xor 0となります。この結果も0。つまり、0同士の排他的論理和のグループは0と置き換えることができます。

f:id:agw:20171004051733p:plain

1のかたまりについても同じように工夫ができるでしょうか? 1と1の排他的論理和は0であることを利用すると先ほどの式は以下のようにまとめることができそうです。1の個数が偶数個であれば、0となることが分かります。

f:id:agw:20171004051741p:plain

1の個数が奇数個である場合も考えてみましょう。

f:id:agw:20171004051746p:plain

連続した排他的論理和の計算結果は1が偶数個あれば0、1が奇数個あれば1となることが分かります。1の数を数えるだけで演算結果が分かってしまうのです。

もしこれまで、検算などをする場合に最初の図のように左から計算していたのであれば是非この方法も試してみてください。計算の速さはもちろん、正確さが格段に上がるはずです。

Idiom: Getting the largest number that is less than x

Algorithm !

Idiom: Getting the largest number that is less than x

プログラムを書いているとき、思ったことが思った計算量でできることは分かっているのに細かい処理がパッと書けないことってありますよね。今日はこの問題を解いているときに、「std::mapのキーがx未満で最大のものを得たい!」と考え至ったのですが、すぐに繰り出すことができず、悔しい思いをしました。

コンテスト中にこういうことが起こるのはよくあります。よくあることなのであればイディオムとしてまとめられるのではないかな、と思いました。

今回のイディオムは以下です。ただし、要素は整列されているものとします。

  • x未満の最大の値を得る

これはO(logN)で行うことができます。具体的には以下のようにします。

  • std::lower_boundでxの下限を探す。反復子が示す要素の一つ前の値が求める値である

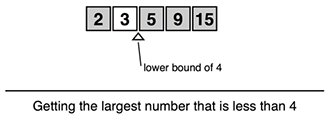
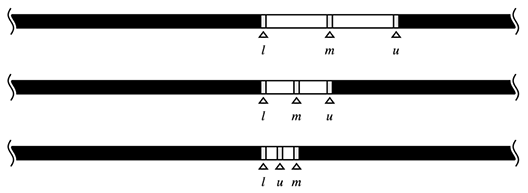
これを図で表せば以下となります。例では4未満の最大の値を探索しています。

要素群にx未満の値がない場合、std::lower_boundは先頭を指し示す反復子を返します。このとき、一つ前の要素にアクセスすることはできないので注意が必要です。


コンテナ独自のlower_boundメソッドを持つstd::setを使って観察してみましょう。std::setの内容は2、3、5、9、15とします。

std::set<int> set = {2, 3, 5, 9, 15};

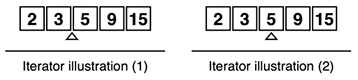
さて、STLの反復子は要素の間を指し示すものとするとすっきりと考えることができるものも多いです。ここからは以下の図の左の表現方法を取りたいと思います。

3未満の最大の値を探してみましょう。lower_boundの結果は以下のようになるため、反復子を一つ戻したものが求める値、2になります。

auto it = set.lower_bound(3);

//  set: 2 3 5 9 15
//        ^
//        `-- it

*(-- it);	// 3未満の最大の値は2

次に9未満の値を探してみましょう。

auto it = set.lower_bound(9);

//  set: 2 3 5 9 15
//            ^
//            `-- it

*(-- it);	// 9未満の最大の値は5

7のように要素として存在しない数値の場合はどうでしょうか? その場合も問題なく動作します。

auto it = set.lower_bound(7);

//  set: 2 3 5 9 15
//            ^
//            `-- it

*(-- it);	// 7未満の最大の値は5

もちろん、21のように大きな値を入れてもきちんと動作します。この場合、itはstd::end(set)を指しますが特に問題はありません。

auto it = set.lower_bound(21);

//  set: 2 3 5 9 15
//                 ^
//                 `-- it

*(-- it);	// 21未満の最大の値は15

最後に先頭の値、例えば、2未満の最大の値を探す場合ですが、これは注意が必要です。itの一つ手間の要素にアクセスすることはできないからです。

auto it = set.lower_bound(2);

//  set: 2 3 5 9 15
//      ^
//      `-- it (= std::begin(set))

*(-- it);	// これはアクセス違反!

そのため、lower_boundを試したあとに反復子が先頭にあるかどうか調べる必要があります。

auto it = set.lower_bound(x);

if (it == std::begin(set)) {
  // x未満の値は存在しない
}
else {
  *(-- it);	// x未満の最大の値
}

イディオムがはっきり見えてきました。aをコンテナとすると以下のように書くことができそうです。

auto it = std::lower_bound(std::begin(a), std::end(a), x);

// または、auto it = a.lower_bound(x)

if (it == std::begin(a)) {
  // x未満の値は存在しない
}
else {
  *(-- it);	// x未満の最大の値
}

二分探索で失敗しないために

二分探索で失敗しないために

範囲を求める整数の二分探索を書いていると混乱するときってありますよね。でも全然書けないわけじゃないんです。すっきり書けることも多い。でも、こういうことがよく起こるんです。

  • 無限ループに陥る
  • 範囲を狭めるとき、下限と上限の何れを更新してよいか迷う
  • 答えが一個ずれている

ごく最近幾つかのコツを掴んでようやく迷わず書けるようになってきました。今後も二分探索で失敗しないためにまとめてみることにしました。

探索の型を見極める

範囲を求める整数の二分探索は大きく2つに分けることができます。これを設計段階で見極めておくことが重要であるようです。

本エントリではそれぞれの型をlower_bound型、upper_bound型と呼びます。C++のSTLで実装されているstd::lower_boundとstd::upper_boundを参考としました。日本語にすれば、下界型(下限型)、上界型(上限型)とでも言うのでしょうか。



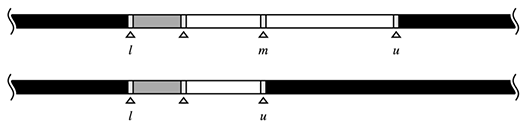
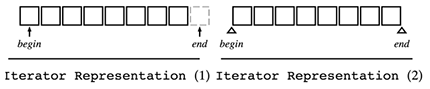
灰色で図示されている要素は「i番目の要素をaiとしたとき、関数f(ai)が真である」ことを表しています。下限と上限は楔(くさび)で表しています。テキストエディタで言えば、「文字と文字の間にカーソルがある」ような位置の考え方です(余談ですが、実際にテキストエディタを設計する場合はこのような位置の考え方をすると設計が簡潔になるそうです)。

続いて、位置が要素の位置にある考え方も図示します。



上の楔型と要素型の図示の間には不整合性がありますが、後で明らかになりますので今は放っておきましょう。

文章でも言い表しておきましょう。

  • lower_bound型
    • 関数f(ai)が真となる最小のiを探索する
  • upper_bound型
    • 関数f(ai)が真となる最大のiを探索する


また、二分探索はその性質上、以下のようなデータには適用できません。


関数f(x)ってなに?

まずは簡単な例で考えてみましょう。整列済みの数値の配列を例にします。


lower_bound型としては以下のような問題を考えます。

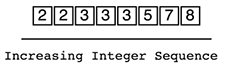
aiが3以上である最小のiを求める

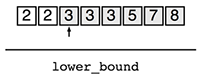
図示すると以下となります。0-indexで考えたとき、2が解となります。



このとき、関数f(x)は以下のような関数となります。

bool f(int x)
{
  return x >= 3;
}


upper_bound型としては次のような問題を考えます。

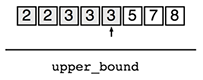
aiが3以下である最大のiを求める

図示すると以下となります。0-indexで考えたとき、5が解となります。



このとき、関数f(x)は以下のような関数となります。

bool f(int x)
{
  return x <= 3;
}

初期範囲を決める

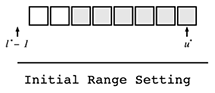
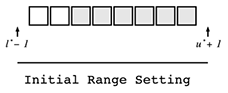
求める解の範囲が分かっている場合、言い換えれば、ある範囲の中に必ずf(ai)が真となるiがある場合は以下のような範囲を用います。ここで、l*とu*はそれぞれ解が取りうる範囲の下限と上限を示します。

図示すると以下のようになります。



範囲を扱う際は右閉半開区間を用います。例えば、i ∈ [0, 7]の範囲に解があることが分かっているのであれば、初期の範囲を(-1, 7]とします。

C++の実装で表すと次のような感じになります。

  int l = -1, u = 7;

右閉半開区間を用いるのは計算機の整数演算を巧みに利用するためで、以下のような特徴があります。

  • 無限ループに陥らない
  • 同じ要素が複数回評価されることがない

反復の条件

二分探索は範囲をしぼり込むことによって探索を行います。範囲から要素がなくなってしまっては意味がありませんのでその直前で反復を停止します。具体的には範囲がただ一つの整数値を表している場合、つまり範囲が(x - 1, x]となったら反復を終了します。C++での実装は以下のようになります。

  while (u - l > 1) {
          :
  }

後でまた触れますが、このように実装したときにf(l* - 1)やf(u*)が評価されることはありません。

範囲を更新する

二分探索は反復毎に範囲を約半分に狭めていくことによってO(logN)の計算量を実現しています。各反復ではまず中央の値を計算します。整数演算ですので、端数は切り落とされます。

中央の値を使い、f(am)を評価します。その結果によって範囲を更新します。

  • mでuを更新する(更新した範囲は(l, m]となる)
  • mでlを更新する(更新した範囲は(m, u]となる)

さて、この節では一先ず細かいことを抜きにしてどのように範囲の更新を行うかを注視したいと思います。そのため、要素を詳細に記した図は一度お休みし、より概念的な図を用いることとします。

範囲を更新する際は、それが全体の範囲のどこにあるか、どの程度の大きさであるか等は意識しないほうがいいです。そのため、左右を切った図とします。lとuに挟まれている区間が注目している区間です(以下の図はuppper_bound型)。



また、更新する範囲は探索の型で異なります。lower_bound型から説明します。

lower_bound型における範囲の更新
  • lower_bound型であり、現在注目しているf(am)が真である場合

mは解かもしれませんが、f(ai)が真となる要素iはmよりも左側にまだあるかもしれません。ですので、左側をさらに詳しく探索します。



もちろん次の図のように、中央の値が求める解である場合もありますが、二分探索の途中でこれを意識する必要はありません。また、むしろ意識しないほうがよいようです。慣れてくると、放っておいてもアルゴリズムがこの解を絞り込んだ範囲に放り込んでくれることが分かってくるからです。


  • lower_bound型であり、現在注目しているf(am)が偽である場合

求める解はmよりも右側にあります。ですので、右側をさらに詳しく探索します。



C++で実装すると以下のようになります。

  if (f(m)) {
    u = m;
  }
  else {
    l = m;
  }
upper_bound型における範囲の更新

さて、ここからはupper_bound型を説明します。

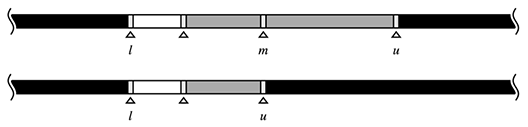
  • upper_bound型であり、現在注目しているf(am)が真である場合

mは解かもしれませんが、f(ai)が真となる要素iはmよりも右側にまだあるかもしれません。ですので、右側をさらに詳しく探索します。



範囲を右閉半開区間として取ることにしたため、mは絞り込んだ範囲に含まれません。ですが心配することはありません。lower_bound型のときと同様に、最後には辻褄がちゃんと合います。

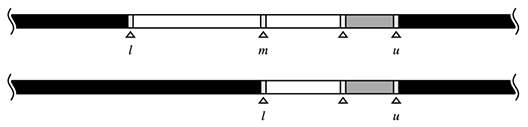
  • upper_bound型であり、現在注目しているf(am)が偽である場合

求める解はmよりも左側にあります。ですので、左側をさらに詳しく探索します。



C++で実装すると以下のようになります。lower_bound型と見比べてみるのもよいでしょう。

  if (f(m)) {
    l = m;
  }
  else {
    u = m;
  }

まずはやってみよう

upper_bound型の場合

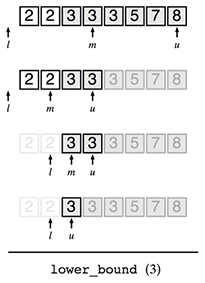
まずはやってみましょう。lower_bound型の二分探索の様子を見てみましょう。C++での実装は以下のようになります。

bool f(int x)
{
  return x >= 3;
}

int lower_bound() {
  int l = -1, u = 7;

  while (u - l > 1) {
    int m = (l + u) / 2;

    if (f(m)) {
      u = m;
    }
    else {
      l = m;
    }
  }

  /* 解は何? */
}


探索の様子を図示してみましょう。



うまく行きましたね! 範囲は最後に(1, 2]となりました(l = 1、u = 2)。範囲の定義からも、図からもuが答えとなることが分かります。

何故こんなにうまく行くのか考えてみましょう。

先ほどの節で説明した通り、lower_bound型の二分探索では現在注目しているf(am)が真であるとき、f(ai)が真となる要素iはmよりも左側にまだあるかもしれないので、左側をさらに詳しく探索します(図を再掲します)。



範囲を右閉半開区間として取るため、mは絞り込んだ範囲に引き続き含まれます。例えばm未満に解がない場合、それ以降どのように探索されたとしても範囲は最終的に(m - 1, m]となります。

f(am)が偽であるとき、f(ai)が真となる要素iは必ずmよりも右側にあります。そのため、右側をさらに詳しく探索します。



範囲を右閉半開区間として取るため、次の範囲(m, u]にmは含まれません。そもそもmは解の候補ではありませんし、lower_bound型の定義からm未満の要素に解はないはずです。そのため思い切って範囲から除くことができるのです。

upper_bound型の場合

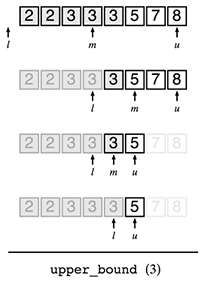
次にupper_bound型の二分探索の様子も見てみましょう。

bool f(int x)
{
  return x <= 3;
}

int upper_bound() {
  int l = -1, u = 7;

  while (u - l > 1) {
    int m = (l + u) / 2;

    if (f(m)) {
      l = m;
    }
    else {
      u = m;
    }
  }

  /* 解は何? */
}


探索の様子を図示してみましょう。



...こちらは微妙ですね。解がlの位置にあります。どうしてこうなったか考えてみましょう。

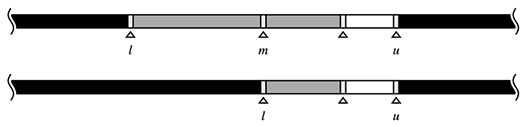
まずf(am)が偽であるときのことを考えてみましょう。mより大きいiのaiには解がありませんので、ばっさりと範囲から除くことができます(図は同じく、再掲です)。



さて、現在注目しているf(am)が真であるとき、それは解の候補となります。つまり、現在の要素、amは真に上限であるかもしれません。ですが、f(ai)となる要素iはmよりも右側にまだあるかもしれないのです。右側を詳しく検索し続ける必要があるはそのためです。


範囲は右閉半開区間として取るのでした。次の期間は(m, u]となります。つまり、一時的に解の候補であるmは範囲から取り除かれます。

ではamが真の上限、つまり解であったとしましょう。ai ∈ (m, u]には解がありませんよね。つまり、(m, u]のどのiの要素に対するf(ai)はすべて偽になります。

そのため、これに続く探索は常に範囲の左側を残すように範囲を絞り続けることとなり、結局のところ範囲は(m, m + 1]となります。求める解はmです。



f(am)が解の候補であるけれども真の上限ではない場合、真の上限となるようなm'を有する区間(l', u']が(m, u]の範囲の中に必ずあるはずですので、やはり右側を詳しく探索します。真の上限となるm'が見つかった場合、範囲は(m', u']を経て(m', m' + 1]となります。この場合の解はm'となります。

本当にうまくいくの?

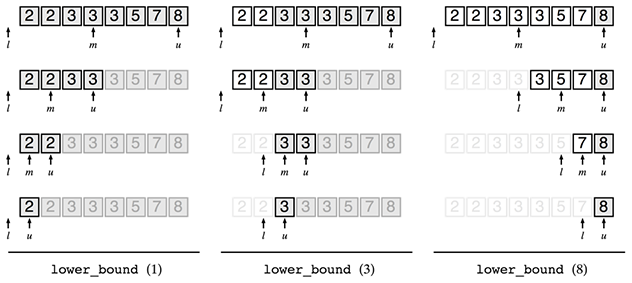
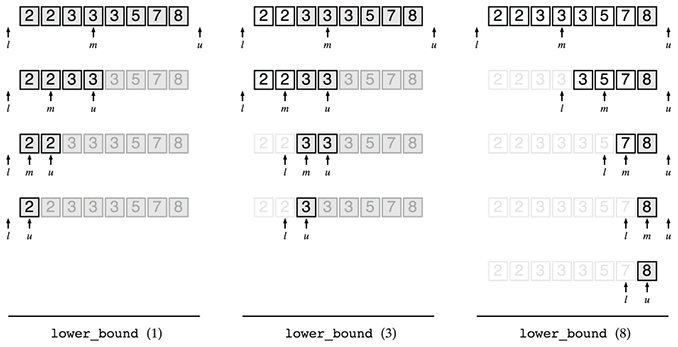
確信を得るために色々な場合の結果を見てましょう。以下はlower_bound型の二分探索を試した結果です。lower_boun型の二分探索の結果はuを見ればよいのでした。それぞれうまく行っているようです。



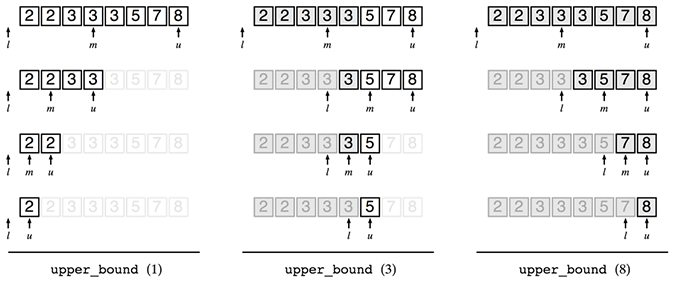
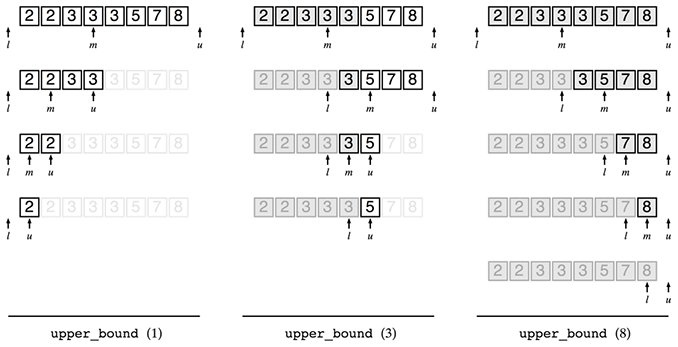
upper_bound型の二分探索も試してみましょう。



upper_bound型の二分探索の結果はlを見ればよいのでした。upper_bound (1)の戻り値が-1となってしまいました。これはなんでしょうか?

よく考えてみると、何れのiを用いても関数f(ai)が真になることはありません。想定していない入力だったのでした。


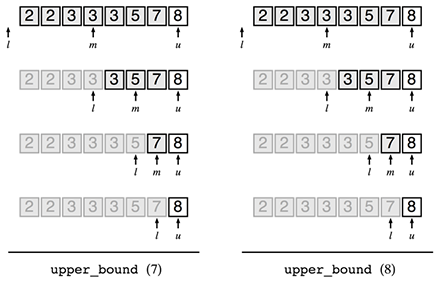
また、upper_bound (8)の結果がおかしいですね。この結果はupper_bound (7)の結果と同じようです。試しに比較してみましょう。



これはおかしいですね。どうしたらよいでしょう?

よりよくするために

まずupper_bound (1)について。これはそもそもupper_bound型の二分探索の定義がおかしかったのです。私たちは以下のように定義したのでした。

  • upper_bound型
    • 関数f(ai)が真となる最大のiを返す

イメージしていたのは以下のような図でした(再掲)。



これを以下のように改訂しましょう。

  • upper_bound型
    • 関数f(ai)が真となる最大のiを探索し、その次の要素を返す

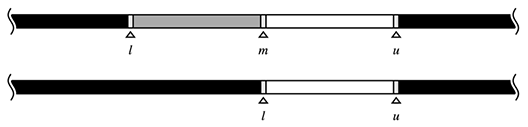
upper_bound型の二分探索のイメージは以下となります。



数値を入れたときの図は以下のようになります。



これでupper_bound (1)の解釈も通るようになりました。以前のようにupper_bound型の探索でf(ai)が真となる最大のiの要素の位置を知りたい場合はlを使うのではなく、u - 1を使うようにします。

これだとどうも分かり辛い、という方は冒頭に記載した楔型の図示をイメージするとよいと思います。



冒頭で少し触れたように、この方法は範囲を表す際によく使われる概念です。

STLのイテレータも楔型で考えると都合がよいものも多いです。std::begin()、std::end()、std::lower_bound()、std::upper_bound()、std::vector::insert()、std::vector::erase()等々...



例えばstd::vector::insert()は楔の位置に指定した要素群が挿入されると考えるとよいですし、std::vector::erase()も楔と楔の間の要素を削除すると考えるとよいかと思います。


話は少々脱線しましたが、次にupper_bound (8)について考えてみましょう。探索の初期範囲を(l* - 1, u*]ではなく、(l* - 1, u* + 1]としてみましょう。

図示すると以下のようになります。



上限を1つだけ大きくしただけですが、これだけで前の節での問題は不思議と解消されます。



もちろんlower_bound型もきちんと動作します。



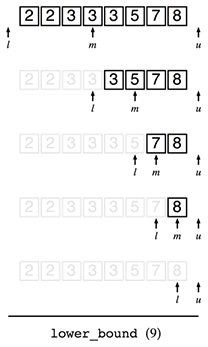
それに加え、lower_bound(9)のように解が存在しないも適切に表現できるようになります。



「f(u* + 1)の挙動はそもそも未定義かもしれないじゃないか。もしかしたらアクセス違反するかも」と思うかもしれません。しかし、右閉半開区間を伴った二分探索ではmがu* + 1となることがありません。そのため、アルゴリズム的な曖昧さはなく、関数f(x)を変更する必要もありません。

またそもそも関数f(x)を解が存在する範囲以上の入力に対応させ、ある程度余裕を持たせた初期範囲を設定するのも常套手段であるようです。

まとめ

このエントリでは二分探索で失敗をしないためのコツを考えてきました。

  • 探索の型を見極める
    • lower_bound型か、upper_bound型か
  • 初期範囲を決める
    • 右閉半開区間を用いる
    • 最低限(l* - 1, u* + 1]を設定する
  • 反復の条件はu - l > 1が成立する間とする
  • 中央値mを算出し、f(am)を評価する
  • 評価の結果によって、範囲を更新する
    • lower_bound型でf(am)が真である場合、(l, m]を次の範囲とする
    • lower_bound型でf(am)が偽である場合、(m, u]を次の範囲とする
    • upper_bound型でf(am)が真である場合、(m, u]を次の範囲とする
    • upper_bound型でf(am)が偽である場合、(l, m]を次の範囲とする
  • 探索の型によって解を選ぶ
    • lower_bound型である場合、関数f(ai)が真となる最小のiはuである
    • upper_bound型である場合、関数f(ai)が真となる最大のiはu - 1である

文章にすると意外に長いですが、実際には実装のテンプレートは決まっています。if文の中身を決定することが出来ればelse句は自然と決まりますので、コツを覚えなければならないのは二ヶ所です。

int {lower|upper}_bound() {
  int l = L, u = U;

  while (u - l > 1) {
    int m = (l + u) / 2;

    if (f(m)) {
      /* lower_bound型ではu = m; */
      /* upper_bound型ではl = m; */
    }
    else {
      /* lower_bound型ではl = m; */
      /* upper_bound型ではu = m; */
    }
  }

  /* lower_bound型ではreturn u; */
  /* upper_bound型ではreturn u - 1; */
}

範囲の更新の部分を思い出すのは簡単です。lower_bound型であるなら、以下の図をちょいちょいと書くだけです(図は再々掲)。



何れの型にしても、f(am)が真となるような図を書くのがポイントのようです。

奥深い二分探索

このエントリはCompetitive Programming Advent Calendar 2015の12/16日分のエントリとして記載しました。

私はこのエントリに記載したコツを使うことによって随分迷わなくなりましたが、二分探索の世界は実に奥深く、様々な「必勝法」が存在し、それに関する議論はいつも尽きないようです。


上位コーダーによる記事はシンプルにまとめられています。よく引用されるエントリには必ず目を通しましょう。


プログラミングコンテストチャレンジブックの存在を忘れてはいけません。本エントリで記載した右閉半開区間を用いるアイデアはこの書籍を読んで得た知識です。プログラミングコンテストチャレンジブックでの二分探索のアプローチは@kinabaさんのアプローチに近いように感じています。


また、私は「ビット逐次決定型」と無理矢理名付けていますが、中央値を求めるような反復を行わず上位ビットから決定していく手法は、二分探索の議論において必ず言及されるようです。二分探索を違った視点から眺めることができますので、ご一読をお勧めします。

また、@hirose_golfさんによる手法は本エントリで取ったアプローチと同様にlower_bound型とupper_bound型を設計段階で意識したアプローチとなっています。しかしながら、lower_bound型とupper_bound型を明確に区別するように紹介しましたが、そのような説明をする記事は少ないように感じます。少し考えるとupper_bound型はf(ai)の否定(つまり! f(ai))が真となる最小のiを探す問題、つまりlower_bound型に置き換えることができるからかなあと考えています。

To a better understanding of the Otsu’s method

Probability !

大津の方法の最も有名な応用例として画像の2値化が挙げられます。この応用での圧倒的ともいえる知名度とその貢献度からか他の問題(例えば機械学習)への応用に関して明示的に言及されることが少ないですが、英語版のWikipediaの記事に記載されているように、その本質は一次元の離散な線形判別分析法の一種です(余談ですが判別分析法という呼び名の他にも判別分別法等、色々な呼び方があるようです)。


大津の方法に関しては画像解析ハンドブックのp. 1520、8 2値画像処理、8.1.2 しきい値自動決定法で詳しく紹介されています。

[2] 大津の方法

大津の判別分析法(Otsu's adaptive thresholding method)とよばれる方法であり、画像の濃淡ヒストグラムから統計的な意味での最適しきい値を決定する。あるしきい値によってヒストグラムを2つのクラスに分割した場合のクラス間分散σB2(k)が最大になるkをしきい値k*に選ぶという原理である。

画像解析ハンドブック

ここで言及されているクラス間分散σB2(k)は以下のように計算される値です。

またNを全画素数、niをレベルiの画素数とします。ここからNとniからレベルiの画素が占める割り合いを算出することができます。これをpiとします。

これらを元に、ω0やω1、μ0やμ1、μτは以下のように定義します。Lは画像全体の諧調数を表します。

これらの式を元に以下の係数ηを最大化するk*を計算します。

右辺の分子は先に挙げた「最大化させる」式です。分母のστ2は全分散です。その名の通り、全体の分散を表します。対象が画像の2値化であれば、画像全体での分散となります。全分散はしきい値にどんな値を設定しても不変なので、ηを最大化するk*を探すときには定数として考えてしまって構いません。先ほどの抜粋では全分散に関して言及されなかったのはこのためです。

画像解析ハンドブックでの大津の方法の解説は以上ですが、これだけだと少し分かり辛いですよね。少なくとも私はそう感じ続けていました。しかし、最近わかりやすいパターン認識という書籍を読み、一気に理解を深めることができました。これを紹介したいと思います。


わかりやすいパターン認識では上述のηを変形したJσ、「クラス内分散・クラス間分散比」を採用し、これを「クラス間分離度」としてしきい値を評価します。

そのためにまず、「クラス内分散」と「クラス間分散」の定義をしています。以下は第5章 特徴の評価とベイズ誤り確率、5.2 クラス内分散・クラス間分散比からの抜粋です。

クラスωiに属するパターン集合をχiとし、χiに含まれるパターン数をni、平均ベクトルをmiとする。また、全パターン数をn、全パターンの平均ベクトルをmとする。ここで、クラス内分散(within-class variable)をσW2、クラス間分散(between-class variance)をσB2で表す

わかりやすいパターン認識

ここで、σW2とσB2は以下とします。

続けて、わかりやすいパターン認識ではクラス内分散とクラス間分散を以下のように説明しています。

クラス内分散はクラスの平均的な広がりを表し、クラス間分散はクラス間の広がりを表している。したがってそれらの比Jσを定義すれば、Jσが大きいほど優れた特徴であると判定することができる。上記Jσはクラス内分散・クラス間分散比(within-class variance between-class variance ratio)と呼ばれる。これはクラス内距離で正規化したクラス間距離とみることもできる。

わかりやすいパターン認識

画像解析ハンドブックで解説されていた大津の方法の式と比べると

  • 連続である
  • 多次元のベクトルを扱っている

という差はありますが、式として圧倒的に見通しのよいものになっていることが分かります。例えばクラス内分散を算出する式は分散(全分散)を算出する式とほとんど変わず、平均値の代わりにそれぞれのクラス(ωi)の平均値miとの差を取ります。逆に言えば、これに模して分散(全分散)の式を書くとすれば以下のようになるでしょう。

クラスに属するデータの分散をσi2とすると、以下のようにも計算できます。

クラス間分散も見た通りです。こちらはクラスに属するデータの平均値の分散を算出しています。クラスの平均値がばらつけばばらつくほど分離度が高いというのは想像と容易に合致することでしょう。


さて、Jσを一見すると、最大化するしきい値を探すときにクラス内分散とクラス間分散の双方を計算しなければならないように見えます。わかりやすいパターン認識ではその点について言及していません。しかし、全分散とクラス内分散、クラス間分散には以下の等式が成り立つことが広く知られているようです。

これを用いると、Jσを以下のように変形することができます。

分散は負の値を取りません。そのためσB2は[0, στ2]の範囲を取ります。この区間でJσはσB2について単調増加する関数ですので、Jσを最大化するしきい値を探すにはσB2を考えれば十分、ということになります(σB2をx、στ2をaとするとJσ = x / (a - x)であり、この微分はa / (a - x)2であることを考えてみるとよいでしょう)。

まとめ

  • クラス内分散、クラス間分散を正確に把握することにより、クラス内分散・クラス間分散比をより深く理解することができる
  • 大津の方法は一次元の離散な線形判別分析法の一種である。そのため、上記を理解することにより迷いなく応用することが期待できる

大津の方法は大変有名な手法で独立して紹介されていることが多く、またアルゴリズムとしてもコンパクトに記述することが可能なことからその式の成り立ちが見えにくいように感じていました。そもそもの成り立ちであるクラス内分散・クラス間分散比から考えていったほうが理解が進むことに気付いたときは目から鱗でした。

機械学習や緩和アルゴリズム等で大津の方法のような簡単な判別分析法が活躍する場面は少なくないように思います。それらの応用についてもいつか時間を取って紹介出来たらいいな、と思います。

さて、本エントリでは以下の2つの書籍の記述を元に文書を構築しました。両書とも大変な良著だと思います。

新編 画像解析ハンドブック

新編 画像解析ハンドブック

わかりやすいパターン認識

わかりやすいパターン認識

中でも画像解析ハンドブックは良著中の良著です。多少値は張りますが機会があったら是非目を通してもらいたい書籍です。

SRM 535 Div II

SRM 535 Div II

  • 初参加したSRMにて惨敗した問題に挑戦。今でも自分には中々難しく、35分ほど時間を要した

FromAndGCDLCM

  • 未知の数AとBの最大公約数と最小公倍数、GとLが与えられる。ここからAとBを推測し、その最小の和(A + B)を返す問題
  • 最大公約数Gと最小公倍数Lに有効なAとBが存在しなければ-1を返す
  • 問題を見てまずぱっと思い浮かべた式は以下だ


  • AとBは[1, 1012]を取る値だ。そのため、上述の左辺が1024を取りうる。これは約1,0008、約280の値だ。素直に実装したらlong longから溢れてしまう
  • さて、上述の式を変形すると、以下となる。


  • 問題に習い、lcm(A, B)L、gcd(A, B)をGとすると、右辺はLGとすることが出来る。
  • AとBを乗してLGとなるようなAとBの組み合わせを求めるような実装は大抵、以下のような形となることが多い。計算量はO(√LG)だ
  for (int i = 1; i * i <= LG; i ++)
                    :
  • さて、この場合、AはGの倍数である。またlong longであることを加味すると、つまり、この実装は以下のような形になると思われる
  for (long long A = G; A * A <= LG; G ++)
                    :
  • LGがlong longに納まりきらないことを承知の上で実装を進めると、以下となる(最大公約数を今一度求めるのは実装をテストして気付いた。サンプルになければWAを出していたところだ)
  long long nm = INF;

  for (long long A = G; A * A <= LG; G ++)
    if (LG % A == 0) {
      long long B = LG / A;

      if (std::__gcd(A, B) == G)
        nm = std::min(A + B, nm);
    }
  • 繰り返すが、A・AやLGはlong longに収まらない。そのため、何らかの回避策を取る必要がある
  • AをiGと表すことにする。iを倍数として、long longから溢れさせないようにする作戦だ


  • 難しいのは反復の条件だ。A = iGとすると、以下とすることができる


  • また、iからBを求めるには以下とする


  long long nm = INF;

  for (long long i = 1; i * i <= L / G; i ++) {
    long long A = i * G;

    if (L % i == 0) {
      long long B = L / i;

      if (std::__gcd(A, B) == G)
        nm = std::min(A + B, nm);
    }
  }

まとめ

  • SRM参戦時に惨敗した問題。解けて素直に嬉しく思うと共に、Div II Mediumとしてはなかなか難しく、またとても良問であったように思えた
  • A、B、lcm(A, B)、gcd(A, B)を考えるとき、以下の関係式は大変重宝する


  • 積がNとなるようなiとjを組み合わせる際の典型の実装は以下となり、その計算量はO(√N)である
  for (int i = 1; i * i <= N; i ++)
    if (N % i == 0) {
      int j = N / i;
            :
    }

SRM 653 Div I

SRM 653 Div I

http://community.topcoder.com/stat?c=round_overview&er=5&rd=16317

SRM 653 Div Iに参加。制限時間一杯Easyを考えるが、全く手が出ず。SRM後に幾つかの実装を読み、全く考えもしていなかった問題に還元できることを学んだ。

グラフの問題であると捉え作図を行ったため、メモの代わりとしてブログ記事として記載した。

CountryGroupHard

http://community.topcoder.com/stat?c=problem_statement&pm=13688&rd=16317

  • 以下のような数の並びが与えられる


  • 数値の周りには同じ数値が、数値分だけ集まる
  • 0は数値が隠されていることを示す
  • 1以上の数値は既知であることを示し、必ず正しい
  • 全体が成立するように、数値を推定したい
  • そのとき既知の数値から隠された数値を一意に推定できるかどうかを判断して回答する問題
  • 例えばこの例は数値が一意に求まり、以下のようなものであったと推定できる


  • 以下も数値が一意に求まる例だ


  • 以下は数値が一意に求まらない例


  • この数列を成立させる組み合わせは複数ある。書き出してみると5種類あった

  • SRMでは多くの参加者がDPもしくはメモ化再帰の問題として解いていたが、全く理解できなかった
  • SRM終了後に幾つかの実装を読み、ようやく理解をすることができた
  • 自分が理解する上で一番しっくりきたのが、経路の組み合わせを数え上げる問題に還元するものであった
  • 先ほどの例で考えてみよう。数値の列として捉えるのではなく、


  • 以下のように成立する経路を考え、その経路を数え上げる問題とするような感覚で捉えるのが自分には合っているらしい

  • さて、実際には上記のように極度に抽象化したグラフではなく、数値群の間に頂点を配置して考えた
    • 初期状態では左端の頂点にのみ経路が設定されていることに注意したい。またその数は1だ


  • 一番左の数値に1を設定してみよう。結果、左端の頂点から次の頂点への経路が成立する。つまり、左端の頂点から次の頂点への経路は少なくとも1種類存在すると言える
    • そのため、二つ右側への頂点へ左端の頂点に到達する経路の数、1を足し込む


  • 一番左の数値に2を設定してみよう。このときは左端の頂点から二つ右側への頂点への経路が成立する。先ほどと同様に、左端の頂点から二つ右側への頂点への経路は1種類存在すると言える
    • そのため、二つ右側への頂点へ左端の頂点に到達する経路の数、1を足し込む


  • 一番左の数値に3を設定してみよう。3の周辺には3つの3が集まるはずだが、隣の数値は2で、条件が成立しない。そのため、経路も成立せず、この場合は左端の頂点から三つ右側への頂点への経路が存在しないことが分かる


  • 左側の頂点からの経路をまとめてみよう。以下のようになる


  • 二つ目の頂点から同様に考える。しかし、この頂点から成立する経路がない


  • 三つ目の頂点からも考えてみよう。以下のように右側の数値群を3で埋めてやると経路が成立することが分かる


  • 三つ目の頂点からの経路をまとめる


  • 四つ目の頂点からの経路を考える。四つ目の頂点からの経路は成立するのだが、そもそも左端の頂点から四つ目の頂点に到達する経路がないため、最終的な経路の組み合わせ数に寄与しない


  • 五つ目の頂点からの経路も同様に寄与しない


  • 結果、左端の頂点から右端の頂点への経路は1種類しかないと言え、問題の答えも一意に推定できるものとすることができる。以下は左端から右端の頂点までの経路をまとめたものだ

  • 以下は成立する例


  • その経路をまとめたもの

  • 以下は成立しない例


  • 結果、左端の頂点から右端の頂点へ到達しうる経路は5種類であることが分かる


  • 確かに書き下した組み合わせの数も5種類であった

まとめ

  • まさか数え上げに還元できる問題であるとは微塵も想像もしておらず、大変驚きであった
  • 次回同様の問題が出たら是非解いて、提出したいところだ

おまけ

SRM後に行った実装(システムテストをパスした)。

class CountryGroupHard {
public:
  std::string solve(std::vector<int> a) {
    int size = a.size();

    long long dp[111] = {0};

    dp[0] = 1;

    For (int i = 0; i < size; i ++)
      for (int j = 1; i + j <= size; j ++) {
        bool valid = true;

        for (int k = 0; k < j; k ++)
          if (a[i + k] && a[i + k] != j)
            valid = false;
        
        if (valid)
          dp[i + j] = (dp[i + j] + dp[i]) % MOD;
      }

    return dp[size] == 1 ? "Sufficient" : "Insufficient";
  };
};