kd-tree Visualization(1)

前回のエントリに引き続き、連続したビット群の総数を求めるアルゴリズムを考える予定でしたが、今回は空間分割データ構造に関するエントリにしました。人力検索はてなに以下のような問題が提示されていたのがきっかけでした。

二次元の値(x, y)をもつ集合P から任意の点p の近似点を検索するアルゴリズムを考えています
高速、低負荷で検索するにはどうしたらいいでしょうか？

条件は次の通りです
１．集合Pはあらかじめ、任意の順番でソートしておける
２．点ｐの近似点にする条件は、margin範囲内で一番近いものとするが、margin値はそのときどきで変わる

ターゲットの言語はjavascriptで、200msぐらいの間隔で検索を続けるつもりです
集合P の個数が 1000 ~ 10000 点くらいだったらどうしますか？

二次元の値(x, y)をもつ集合P から任意の点p の近似点を検索する… - 人力検索はてな

私もコメントにてid:pacticalschemeさんが挙げられていた「四分木」、「kd木」あたりを思い浮かべました。しかし、id:you_gotさんが例として掲載した座標群を与えた場合に、kd木がどのように構築されるかすぐに想像出来ませんでした。

(1,1), (1,2), .... (1, 100)
(2,1), (2,2), .... (2, 100)
(3,1), (3,2), .... (3, 100)
(4,1), (4,2), .... (4, 100)
(5,1), (5,2), .... (5, 100)

二次元の値(x, y)をもつ集合P から任意の点p の近似点を検索する… - 人力検索はてな

実際のデータはもっと分散したものなのでしょうが、例に挙げられたこの座標群は極端に整列していますね。

さて、kd木は古典とされる空間分割データ構造で、珠玉のプログラミングといった著書で有名な、あのJohn Louis Bentleyから1975年に発表されており、1980年代に書かれた名著アルゴリズム Cにも取り上げられています。日本語版では、第2巻、計算幾何の領域検索の章に掲載されています。以下はアルゴリズム Cから抜粋したkd木のコードです。書籍では解説と共に進行していくので、これらのコードを単純に組み上げても実際に動作するコードにはなりませんが、検証コードの元として十分なものです。今回は以下のコードを元にPythonで記述しています。

struct node { struct point p, struct node *next; };

struct node *z;

tree2Dinsert(struct point p)
{
  struct node* f;
  int d, td
  for (d = 0, t = head; t != z; d != d) {
    td = d ? (p.x < t->p.x) : (p.y < t->p.y);
    f = t; t = td ? t->l : t->r;
  }
  t = (struct node*)malloc(sizeof *z);
  t->p = p; t->l = z; t->r = z;
  if (td) f->l = t; else f->r = t;
}

preprocess(struct point p[], int N)
{
  int i;
  p[0].x = 0; p[0].y = 0; p[0].info = 0;
  z = (struct node*)malloc(sizeof *z);
  z->l = z; z->r = z; z->p = p[0];
  head = (struct node*)malloc(sizeof *head);
  head->r = z; head->p = p[0];
  for (i = 1; i <= N; i ++) tree2Dinsert(p[i]);
}

一般的にアルゴリズム Cで紹介されているように要素の追加のみでkd木を構築するとバランスの悪い木となることが知られていますが、まずはアルゴリズム Cで取られているアプローチに合わせてみることにします。コードが正しいかを確かめるために、以下のような座標群を用いました。こちらもアルゴリズム Cに合わせ、x、y双方の要素を1より大きい整数値としました。

[(85, 76), (43, 26), (52, 41), (79, 31), (48, 59), (91, 51), (29, 76), (62, 26),
 (91, 99), (82, 91), (32, 73), (90, 69), (48, 11), (44, 62), (92, 97), (48, 87),
 (27, 81), (55,  2), (72, 40), (83, 67), ( 1, 50), (87, 25), (33, 88), (20, 57),
 (24, 97), (81, 45), ( 9, 33), (51, 94), (11, 56), (71, 55), (82, 55), (97, 61)]

この頂点群は、Pythonで以下のように生成しました。

>>> from random import seed, randint
>>> seed(0)
>>> [(randint(1, 100), randint(1, 100)) for i in range(32)]

画像にすると、こんな座標群です。座標に振られている番号は、1から始まる座標群のインデックス値です。

では、2d木を構築してみます。

#/usr/bin/python -t

from random import seed, randint

def insert(tree, pt):
    t = tree
    d = 0
    while t:
        td = 1 if (pt[d] > t[-1][d]) else 0
        f = t
        t = t[td]
        d = (d + 1) % 2
    f[td] = [None, None, pt]

if __name__ == '__main__':
    seed(0)
    pts = [(randint(1, 100), randint(1, 100))
           for i in range(32)]

    tree = [None, None, (0, 0)]
    for pt in pts:
        insert(tree, pt)

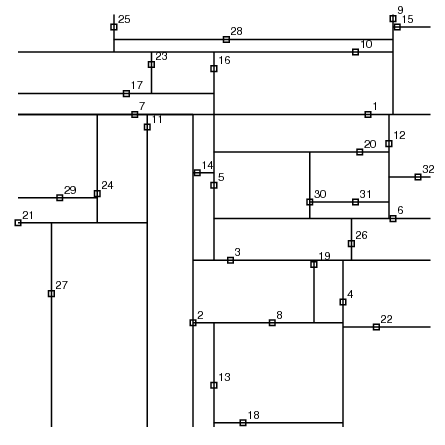
結果をPostScriptで可視化してみます。先ほどと異なり座標に振られている番号は、kd木に挿入された順番を表しています。ただしこの場合は逐次座標を挿入しているため番号の並びは変わっていません。

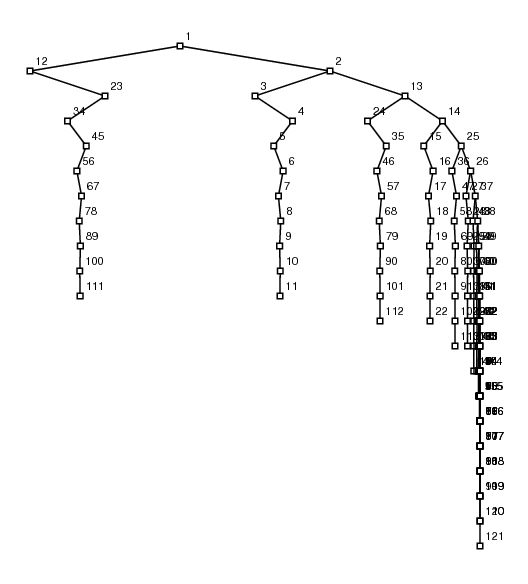
やはりバランスが悪そうですね。このままではよく分からないので、木表現として可視化してみました。

1番の接点の左右にぶら下がっている2番と9番の接点を比べると、2番により多くの接点がぶら下がっていますね。バランスの悪さを客観的に観測することが出来ました。バランスの取れたkd木の検索の計算量はO(log N)と言われていますので、接点数が32個のこの木では5回になるはずです。しかし、この状態のkd木では、31番の座標を検索するのに9回計算しなければならなさそうですね。

バランスの良いkd木を構築する一つのアイデアとして、座標群のメディアンで分割していく方法がありますが、それはまた次回以降のエントリで記載するとして、id:you_gotさんが挙げていた極端に整列している座標群を与えて2d木を構築してみました。1刻みの座標群では可視化した際に煩雑となるため、10刻みで座標群を生成します。

[( 1, 1), ( 1, 11), ... , ( 1, 91), ( 1, 101),
 (11, 1), (11, 11), ... , (11, 91), (11, 101),
     :        :      :        :         :
 (81, 1), (81, 11), ... , (81, 91), (81, 101),
 (91, 1), (91, 11), ... , (91, 91), (91, 101)]

Pythonで上述の座標群を生成するには、以下のようにします。

>>> [(x, y) for x in range(1, 101+1, 10) for y in range(1, 101+1, 10)]

可視化したものは、以下です。何やら大変なことになっていますね。

木表現として可視化したものは以下です。いやはや、バランスが悪い。

バランスの取れたkd木の場合、検索の計算量は7回ほどですが、この状態だと最悪21回の計算量となっています。

次回はメディアンを加味したkd木の構築が如何ほどバランスを改善するかを可視化したいと思います。

アルゴリズムC〈第2巻〉探索・文字列・計算幾何

フォトンマッピング―実写に迫るコンピュータグラフィックス

珠玉のプログラミング―本質を見抜いたアルゴリズムとデータ構造

追記

kd-tree Visualization(2) - agwの日記として続編を記載しました。

追記

Consistent Binary Tree Layout(1) - agwの日記にて、二分木の描画方法を考察しました。