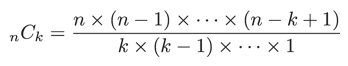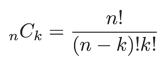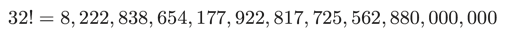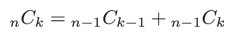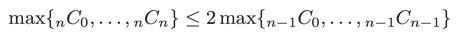Precalculating a Combination
異なるn個のものから異なるk個のものを選ぶ組み合わせは以下のように計算することができます。
階乗を使うとより簡潔に書くことができます。
とてもシンプルに見えますよね。しかし、計算機で組み合わせの計算を行うのは意外と厄介なのです。階乗はとても大きな値になるからです。例えば、32!は以下のような結果になります(決して大きいとは言えない32個の数字を掛けただけなのに!)。
unsigned long longで表すことのできる数値の限界が18446744073709551615、つまり1.8e+19ほどであるのに比べ、32!は8.2e+33です。多倍長整数をサポートしない処理系で、例えば32C16を階乗を用いて計算するのはとても難しいのです。
さて、nCkは漸化式を用いても計算することができます。
漸化式を使えば階乗を使う必要がありません。また漸化式を眺めると和算しか使っていないことが分かります。そのため、計算の途中に結果より大きな値に出くわすことがない、と考えることができます。
そのため、漸化式の特徴を考慮して、ある程度の組み合わせの数を予め二次元配列に計算しておく手法がよく使われています。
nck = [[0] * 111 for i in range(111)] nck[0][0] = 1 for i in range(1, 100 + 1): nck[i][0] = nck[i][i] = 1 for j in range(1, i): nck[i][j] = nck[i-1][j-1] + nck[i-1][j]
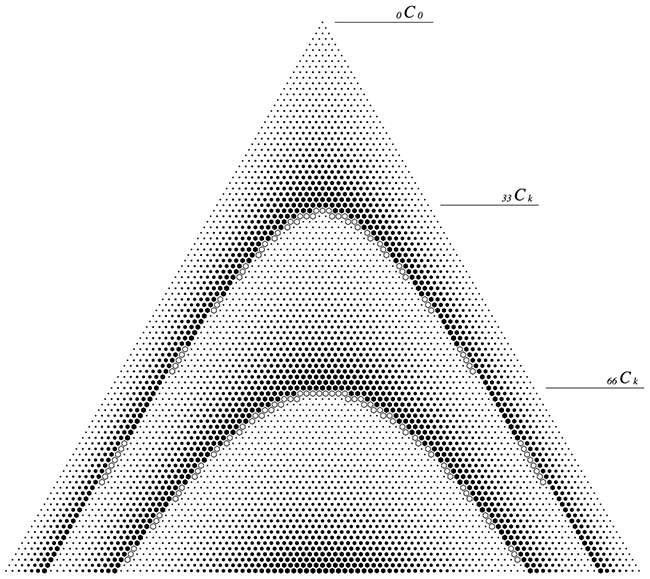
Pythonは多倍長整数が扱えるため、オーバーフローを考えずに100Ckまでの値を計算させてしまいました。しかし、C++等では選んだ整数の型によって比較的すぐオーバーフローしてしまうはずです。この限界をしっかり把握するため検証を行い、結果を図にしてみました。
組み合わせの数を三角形状に並べたものはパスカルの三角形として知られています。パスカルの三角形の最初の10段は以下のようになっています。先の図には数値が記載されていませんが、同じように並べていると考えてください。
結果、int型は0 ≦ n ≦ 33までのnCkが、また、long longでは0 ≦ n ≦ 66までのnCkが扱えることが分かりました。
また、nはそれぞれの型のビット数に近い値であることも分かりました。漸化式からnCkの最大値はn-1Ckの最大値の高々2倍の大きさにしかならないことが分かるので、まあ納得です。
まとめ
組み合わせの数を扱う場合はこの限界値を元に、効率的に考察を行うことが出来そうです。
- nが33までのnCkはintの二次元配列で予め計算しておくことができる
- nが66までのnCkはlong longの二次元配列で予め計算しておくことができる
計算式によっては、漸化式を用いずに階乗を約分して算出したほうが有利な場合もあるでしょう。また、誤差の許容量によっては対数空間での計算や、また、lgamma関数を使うことを検討してもよいでしょう。
何れにせよ組み合わせの数を用いた計算は実装時に大きな数の扱いで困ってしまうことが多いので、適切な戦略を立ててから実装を始めることが肝心なようです。
組み合わせの数を二次元配列で予め計算しておく方法は正直苦手意識を感じていました。ですが今回の考察で少し自信を持って考えることが出来るようになったと思います。