Embedding sed script into Makefile
何らかの目的があって複数のシェルスクリプトを書き殴る必要があるとき、Makefileにシェルスクリプトをガシガシ埋め込んでいくことが多いです。偽のターゲット(Phony Target)でmakeをラウンチャのように使えますし、ファイルの依存関係も見てくれます。並列化の恩恵を受けることも。何より一つのファイルになっているので見通しがよいように感じます。
シェルスクリプトをMakefileに埋め込む際に注意することはさほど多くはありません。
- 各行頭はタブで始める。タブは削除される
- 1行シェルを複数行で書くときは行末に\(バックスラッシュ)を置く。\と改行文字は空白文字へと変換される
- $は$ $として記載する。$ $は$へと変換される(Markdown記法とMathjaxが誤変換してしまうため$の間に空白を入れていますが、本来はありません)
具体的には以下のような内容になるでしょう。ここでは1〜10までの数値\(i\)とその二乗の数\(s = i^2\)を表示します。
doit: Makefile seq 1 10 | while read i; do \ s=`echo $$i 2 ^ p | dc`; \ echo "$$i $$s"; \ done
これは以下のような1行シェルに変換され、サブシェルで処理されます。
seq 1 10 | while read i; do s=`echo $$i 2 ^ p | dc`; echo "$$i $$s"; done
さて、これをsedのスクリプトでもやりたいと常々思っていました。GNU sedであれば1行でループを含んだスクリプトが書けるので(書けそうなので)問題なさそうなのですが、macOSに付属しているBSD sedでは明示的に改行を含んだスクリプトを記述しなければならないらしく、とても厄介です。今回用意したsedスクリプトは行末が,(コンマ)で終わっている行を次の行とつなげる簡単なものです。
:loop /,$/ { N s/\n/ / b loop } p
ここは好みなのですが、自分はsedスクリプトを含んだシェルスクリプトを用意した方が他のシェルコマンドを応用できるため自由度が高く、また保守性も高いように感じています。
#!/bin/sh sed -ne ' :loop /,$/ { N s/\n/ / b loop } p '
以下のようなファイルに対して適用すると、
1, 2, 3 4, 5
以下のような出力を得ます。
> ./sample.sh < sample.txt 1, 2, 3 4, 5
さて、ある程度大きいsedスクリプトにならないとき、これをMakefileに埋め込んめてしまえればなあと思うことが少なくありませんでした。重い腰を上げて色々と試してみたのですが、決定打のようなものは打ち出せませんでした。およそ綺麗とは言い難い解決法ですが、備忘録として記載しておきます。
ヒアドキュメントを記述する際は、
- $は$ $に置き換える
- makeが展開する際に1行として認識するように、行末に\を付ける
- echoが展開する際に改行がなされるように行末に\nを付ける
- \nなどは\\\\n等に置き換える
define SED_SCRIPT :loop\n\ /,$$/ {\n\ N\n\ s/\\\\n/ /\n\ b loop\n\ }\n\ p endef doit: a.sed sample.txt cat sample.txt | \ sed -n -f a.sed a.sed: Makefile echo "$(SED_SCRIPT)" > $@
echo文で記載されている"(ダブルクォート)はとても大事です。これがないと\nは思ったように展開されません。つまるところ、makeはsedスクリプトを書き出す際に以下のことをしています。分かれば仕組みは簡単ですね。
echo ":loop\n /,$/ {\n N\n s/\\\\n/ /\n b loop\n }\n p" | sed -e '2,$s/^ //' > a.sed
ちなみに書き出されたsedスクリプトはmakeによる行末の\と改行文字を空白に直すこと、またechoコマンドの副作用のせいで空白の意味合いが変わってきてしまっています。あまりよくないですね。
:loop /,$/ { N s/\n/ / b loop } p
When does grep -v succeed?
昨日、簡単なシェルスクリプトを書いていたとき、「grepはマッチする行が1行でもあれば真を返すのであった。はて、grep -vの戻り値はどういう条件で真になるんだろう? また、grep -v -e a -e bなどといったように、条件が複数指定されているときはどうなるのだろう?」と悩んでしまいました。
調べた結果、「grepに-vフラグが指定されているときは、マッチしない行が一行でもあると真を返す」ようです。そこからの結論として、「grepは、-vフラグの指定の有無に関わらず、表示される行がある場合に真を返す」ということになります。
...とここまで時間をかけて検証をしたのですが、マニュアルにきちんと記載されていることに気づきました。マニュアルは機会があるごとに積極的に読まないと結局損をしますね。
EXIT STATUS
The grep utility exits with one of the following values:
0 One or more lines were selected.
1 No lines were selected.
>1 An error occurred.
Idiom: Passing reverse iterator to a constructor
文字列\(s\)から反転した文字列\(t\)を作成するとき、これまではコピーして反転という処理をしていました。
std::string s("string"); : std::string t(s); std::reverse(ALL(t)); // tの内容は"gnirts"となる
今日なんとなくこの実装を見て目から鱗が落ちました。コンストラクタにリバースイテレータを渡してしまえばいいんですね。この発想はなかった。
std::string s("string"); std::string t(s.rbegin(), s.rend()); // tの内容は元々"gnirts"となる!
「何かを反転したもの」を得たいことはよくあるのでこの手法はこれから活躍しそうです。
Using std::multiset instead of std::priority_queue
std::multisetをstd::priority_queueの代わりに使う実装例を目にしました。std::priority_queueは重いと言われているし、std::multisetのほうが性能がよいのであれば使う価値があるな...と考えて計測してみたところstd::priority_queueよりも3倍重く少しがっかり。まあ知見は得られたのでよしとします。
以下は検証に使った実装です。こちらはstd::priority_queueを使ったもので、数値の小さいものをキューに残そうとします。値が重複していても大丈夫です。
int N = 1000000, M = 100, K = 1000; std::priority_queue<int> pq; for (int i = 0; i < N; i ++) { // N回 int size = rand() % M; for (int j = 0; j < size; j ++) // [0, M)個のランダムな値を追加して pq.push(rand()); while (pq.size() > K) // キューがK個になるまで大きな数値を取り除く pq.pop(); // (つまり、小さな数値を最大K個残す) }
std::multiset版はこちらです。数値の小さいものを残すために値の正負を反転しています(std::multiset::removeがリバースイテレータを取れればいいのですが、そういうものではないようです)。
std::multiset<int> set; for (int i = 0; i < N; i ++) { int size = rand() % M; for (int j = 0; j < size; j ++) set.insert(- rand()); while (set.size() > K) set.erase(std::begin(set)); }
それでもstd::multisetを使う利点があるとすれば、要素を取り出すことなく反復できるところでしょうか(std::priority_queueは取り出す必要があります)。
// 要素を(結果、降順で)表示する for (const auto& i : set) std::cerr << - i << std::endl;
Visualizing Rank on Union-Find Tree
縮約を伴ったUnion-Find木は高速に動作することで知られています。以下は蟻本からの抜粋です。
// 木の根を求める int find(int x) { if (par[x] == x) { return x; } else { return par[x] = find(par[x]); } } // xとyの属する集合を併合 void unite(int x, int y) { x = find(x); y = find(y); if (x == y) return; if (rank[x] < rank[y]) { par[x] = y; } else { par[y] = x; if (rank[x] == rank[y]) rank[x]++; } }
木の根を求める際、同時に縮約を行い、また併合の際にはランクを使って木の高さに偏りが発生するのを抑えます。
同時に蟻本には以下のように注記がなされています。
縮約を行って木の高さが変化しても、簡単のため rank を変えることは考えません。
ランクの概念や制限も大体理解しているつもりでしたのでライブラリにほぼ写経した実装を押し込み、習得したものとしていました。ですが、先日参加したコンテストでこの実装を見て、憧れの念が生まれました。ランクを使いこなしている。そう感じたからです。
早速蟻本の実装を見直しました。理解していたつもりがスラスラと読めない...後からでも正確にイメージできるように作図することにしました。
- 木のランクが異なる場合、ランクの小さい木の根からランクの大きい木の根に辺を張る
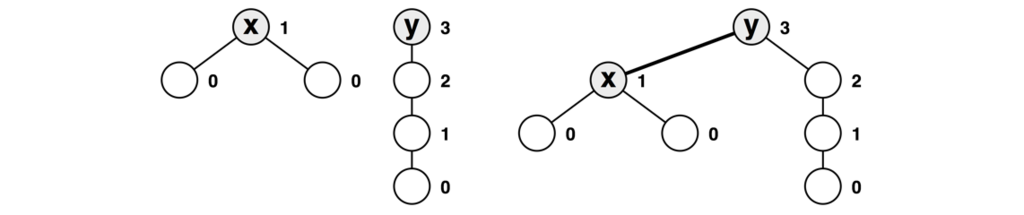
例えば以下のxとyの頂点を併合することを考えます。頂点の右の数値はランクを表しています。xのランクは1、yのランクは2です。そのため、右のように辺を張ります。

\(\mathit{rank}_x < \mathit{rank}_y\)ですので、\(\mathit{rank}_x + 1 \le \mathit{rank}_y\)が常に成り立ちます。ですので、yのランクを更新する必要はありません。
同様に木のランクが異なる場合の例です。
- 木のランクが同じ場合、片方の木の根から他の木の根に辺を張る。そのとき、辺を張られるほうの木のランクを1つ増やす
以下の例でもxとyの頂点を併合することを考えています。双方の木のランクは同じですので、この場合はxからyに辺を張ってみることにしましょう。ランクは2になります。

ランクが同じときの辺の張りかたも統一しておくとよいでしょう。ここでは蟻本を見習って、「根のインデックスが大きいものから小さいものに辺を張る」ことにしましょう。これに習うと上の例は以下のようになります。

さて、併合時に縮約が起きる様子も見てみましょう。以下は、多少作為的ですが、蟻本の実装ではこうはならない、という例です。今回はzとaを併合します。
zの根を求める際に縮約が発生します(中央の図)。aの根はaですので縮約は発生しません。結果的に、xとaを併合します。

さて、どこが作為的なのでしょうか? 実はこれ、縮約された木のランクを意図的に操作しているのです。これまで行儀のいい場合のみ図示してきましたが、蟻本の実装では縮約の際にランクを操作しません。そのため、実際には以下のようになります。
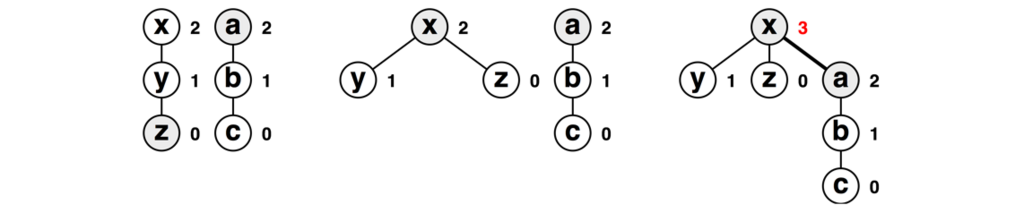
併合時に参照されるランクは根のものだけであることに注意してください。言い換えると、一回子供になってしまった頂点のランクはもう気にする必要はありません。少々乱暴ですが、縮約は根の参照の効率を改善するためだけに行われていると言ってもいいでしょう。
蟻本の例には以下のような縮約の例が掲載されています。具体的にはeをfindするとこのような縮約が発生します。
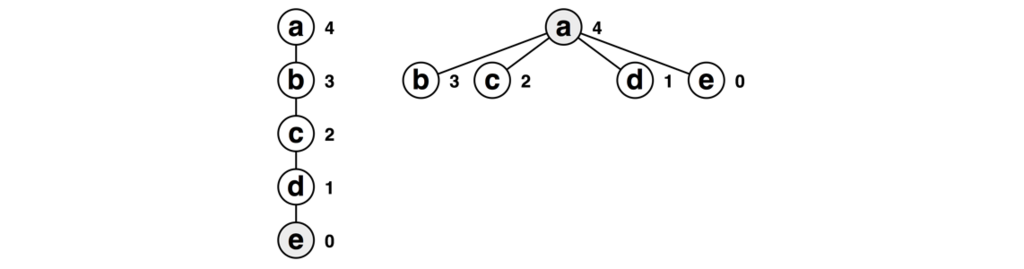
蟻本の図にはランクが示されていません。そのため、図からこのようなことが起こっていると捉えてしまっている人は少なくないかもしれません。
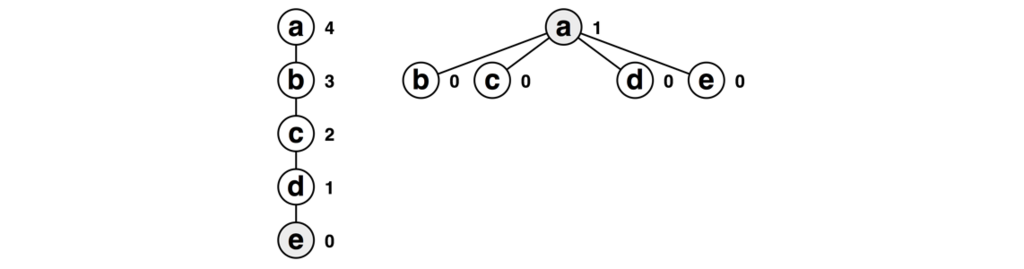
また、木の中腹の頂点をfindすると以下のような縮約が発生します。これはcをfindした例です。
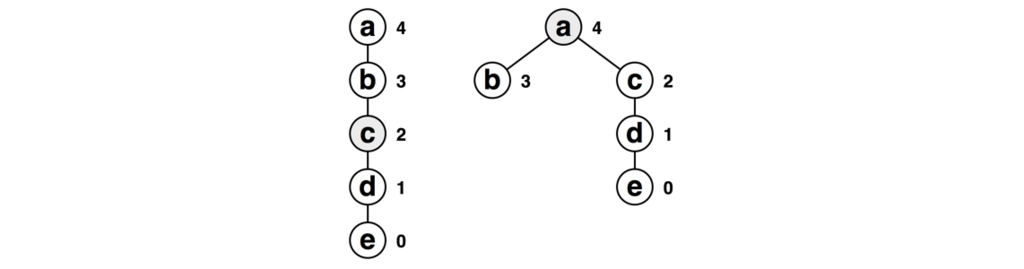
最後に、ここまでの図にはランクが2の木が出てきていました。では実際にランク2の木はどのように作ることがができるでしょう? ランクを2にするには、ランク1の木が二つないといけません(おそらく、今まで説明に使ったx、y、zの3頂点からなる木は作れないように思います)。

Idiom: Partial Sorting
書庫から久しぶりに取り出したEffective STLをパラパラめくっていて、std::partial_sortのうまい用法を学びました(第31項「ソートの選択肢を知っておこう」)。昇順に整列して初めから20番目の要素までの合計を取りたいときにはstd::sortを使うより、std::partial_sortを使ったほうが効率的であるようです。
std::vector<int> a; // ...aを更新する std::partial_sort(std::begin(a), std::begin(a) + 20, std::end (a)); int sum = std::accumulate(std::begin(a), std::begin(a) + 20, 0);
イテレータを3つ取る関数には苦手意識がありましたが、この用法は覚えやすいですし、手軽な定数倍高速化として重宝するかもしれません。計算量は面白く、
$$ O({}(\mathrm{last} - \mathrm{first})\log(\mathrm{middle} - \mathrm{first}){}) $$
だそうです。線形の項が配列全体の要素数なので劇的に計算量が減るわけではなさそうですが、以下のように一定の効果は期待できそうです。
$$ \begin{array}{cccc} \mathrm{first} & \mathrm{middle} & \mathrm{last} & \text{Complexity}\\ \hline 0 & 10 & 1000 & 1000 \times 3.322\\ 0 & 100 & 1000 & 1000 \times 6.644\\ 0 & 500 & 1000 & 1000 \times 8.966\\ 0 & 1000 & 1000 & 1000 \times 9.966\\ \end{array} $$
よしよし、一つ賢くなったぞ...と喜んでいたのも束の間、合計を取りたいのであればstd::nth_elementで十分であることに気づきました。std::nth_elementはstd::partial_sortと書式がほとんど一緒ですが、std::partial_sortが先頭から20要素までに上位20個の要素を整列して格納するのに比べ、先頭から20要素までに上位20個の要素を格納する、とのこと。
std::vector<int> a; // ...aを更新する std::nth_element(std::begin(a), std::begin(a) + 20, std::end (a)); int sum = std::accumulate(std::begin(a), std::begin(a) + 20, 0);
(この用途では1)計算量はstd::parital_sortに比べとても効率的で、\(O(\mathrm{last} - \mathrm{first})\)だそうです。\(\log\)が落ちてしまうんですね。
Multi-start Breadth First Search
先日参加したコンテストで以下のような問題が出題されました1。
シンプルなグラフがある。それぞれの頂点は最大で100個ほどのグループに分けられている。各頂点から各グループの頂点までの最短距離を求めよ。ただし、頂点の最大数は\(10^{5}\)である。
この問題、コンテスト中には全く手が出ませんでした。それぞれの頂点から幅優先探索を行なって任意のグループに属する頂点に出会う度に記録すれば、目的はまあ達成です。ですが、計算量は軽く見積もっても\(O(N^{2})\)。\(10^{10}\)を超えてしまいます。これは駄目です。
また、制約から考えると、\(10^{5} \times 100\)のテーブルを用意して記録していけばよいように思うのですが、うまく埋めていくことができませんでした。
このときは次のように考えていました。
- 各頂点から幅優先探索を行う。訪れた頂点のグループ情報を得る。そのグループに初めて訪れているなら、距離を最短距離として記録する(全てのグループに出会ったらその頂点に関しての探索は終了する)
さてコンテスト終了後に色々考えても計算量が落とせなかったので他のコンテスタントの実装を読んでみました。皆幅優先探索を実装しているようですが、探索をグループの数分しか行なっていません...はて?
ポイントは以下でした。
なるほど、これなら計算量も\(O(MN)\)に落とすことができます。「多点開始幅探索」、とでも呼称できそうな技法です。
以下のような盤面を考えてみます。ここで、グループは4色の色として表しています。また、グラフは表示されているよりも広く存在しています。

単点開始幅優先探索では以下のように探索を行います。この緑色の頂点はすぐに、青色と紫色の点を見つけることができますが、赤色の頂点にたどり着くまでには3ステップかかっていることが分かります。
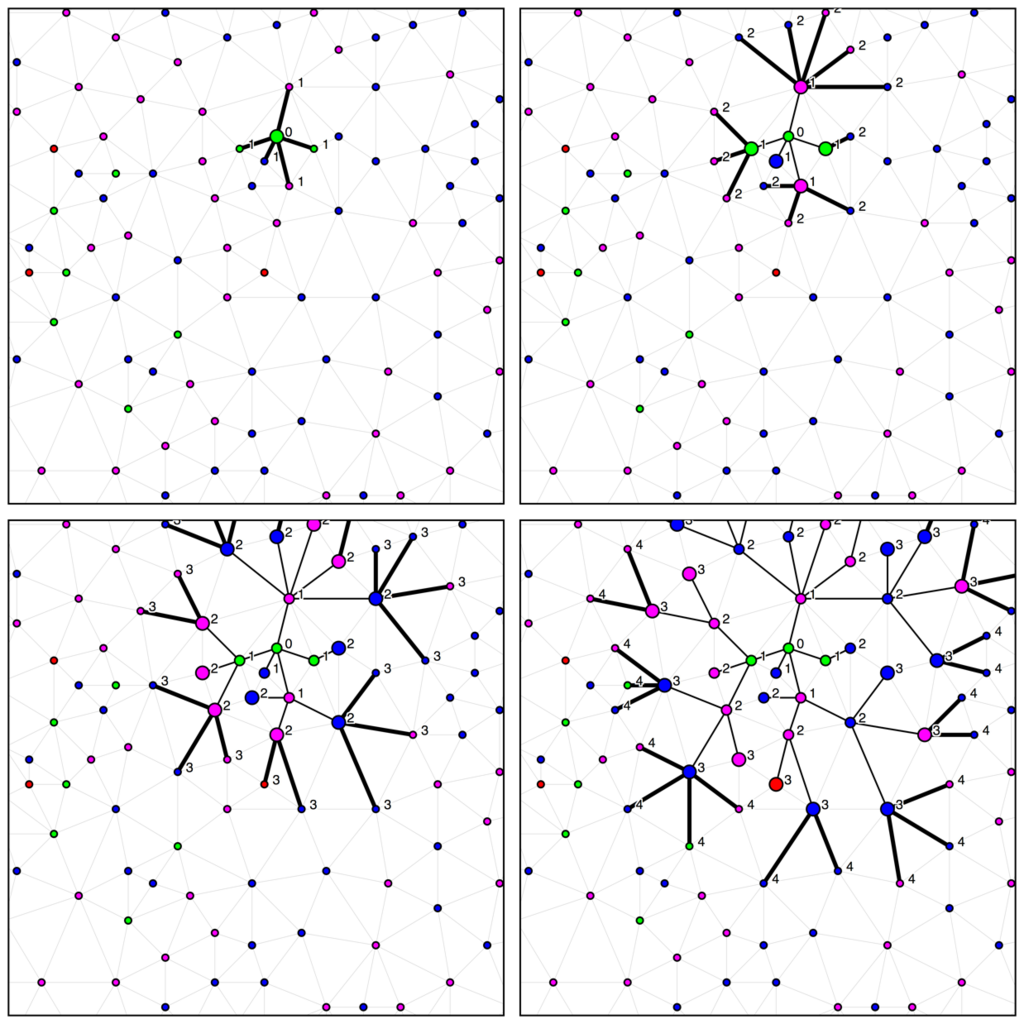
赤色の頂点にたどり着いた時点で自分が属する色以外の3色の頂点にたどり着いたのでここで探索を打ち切ることはできますが、最悪\(O(N)\)の探索を\(N\)回繰り返さなければならないので、計算量は依然\(O(N^{2})\)と考えたほうがよいでしょう。
では多点開始幅探索を見て見ましょう。探索は以下のようになされているようです。先ほどの単開始点から行う幅優先探索に比べて、ほとんどの頂点をすぐ網羅することも注目しましょう。
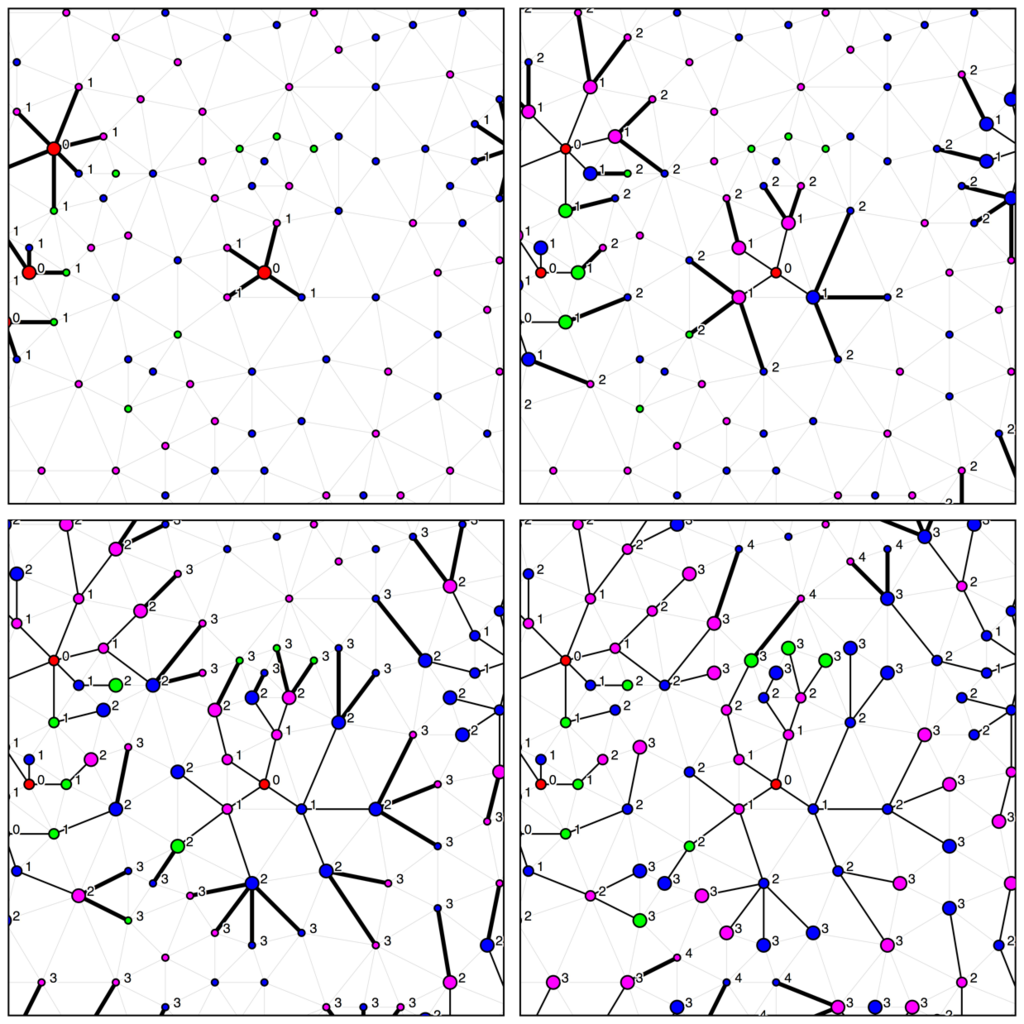
一回の探索で訪れる頂点の数は単点開始でも多点開始でも\(N\)ですが、探索を全体で\(N\)回(最大\(10^{5}\)回)やらなければいけないか、\(M\)回(最大100回)でいいのかで総合的な計算量は大きく変わります。ぜひ覚えておきたい技法です。
-
少し簡潔な問題としています↩