Visualizing Rank on Union-Find Tree

縮約を伴ったUnion-Find木は高速に動作することで知られています。以下は蟻本からの抜粋です。

// 木の根を求める
int find(int x) {
  if (par[x] == x) {
    return x;
  } else {
    return par[x] = find(par[x]);
  }
}

// xとyの属する集合を併合
void unite(int x, int y) {
  x = find(x);
  y = find(y);
  if (x == y) return;

  if (rank[x] < rank[y]) {
    par[x] = y;
  } else {
    par[y] = x;
    if (rank[x] == rank[y]) rank[x]++;
  }
}

木の根を求める際、同時に縮約を行い、また併合の際にはランクを使って木の高さに偏りが発生するのを抑えます。

同時に蟻本には以下のように注記がなされています。

縮約を行って木の高さが変化しても、簡単のため rank を変えることは考えません。

ランクの概念や制限も大体理解しているつもりでしたのでライブラリにほぼ写経した実装を押し込み、習得したものとしていました。ですが、先日参加したコンテストでこの実装を見て、憧れの念が生まれました。ランクを使いこなしている。そう感じたからです。

早速蟻本の実装を見直しました。理解していたつもりがスラスラと読めない...後からでも正確にイメージできるように作図することにしました。

• 木のランクが異なる場合、ランクの小さい木の根からランクの大きい木の根に辺を張る

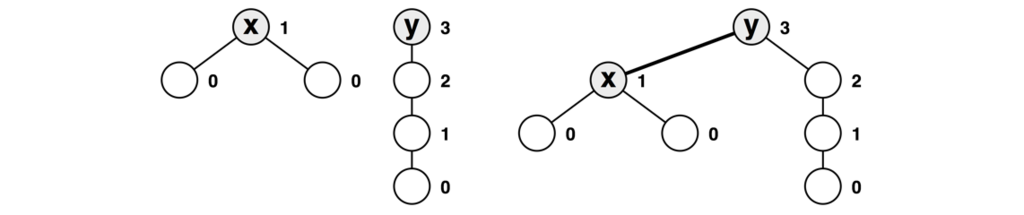
例えば以下のxとyの頂点を併合することを考えます。頂点の右の数値はランクを表しています。xのランクは1、yのランクは2です。そのため、右のように辺を張ります。

\(\mathit{rank}_x < \mathit{rank}_y\)ですので、\(\mathit{rank}_x + 1 \le \mathit{rank}_y\)が常に成り立ちます。ですので、yのランクを更新する必要はありません。

同様に木のランクが異なる場合の例です。

• 木のランクが同じ場合、片方の木の根から他の木の根に辺を張る。そのとき、辺を張られるほうの木のランクを1つ増やす

以下の例でもxとyの頂点を併合することを考えています。双方の木のランクは同じですので、この場合はxからyに辺を張ってみることにしましょう。ランクは2になります。

ランクが同じときの辺の張りかたも統一しておくとよいでしょう。ここでは蟻本を見習って、「根のインデックスが大きいものから小さいものに辺を張る」ことにしましょう。これに習うと上の例は以下のようになります。

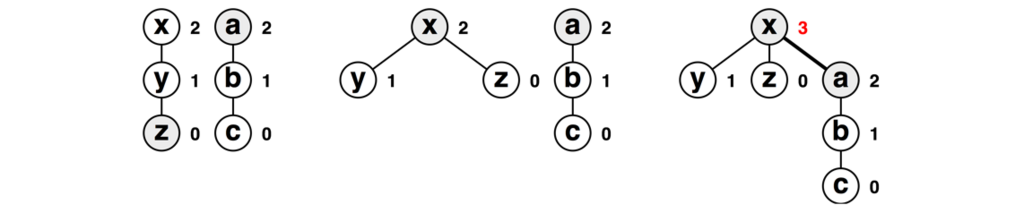
さて、併合時に縮約が起きる様子も見てみましょう。以下は、多少作為的ですが、蟻本の実装ではこうはならない、という例です。今回はzとaを併合します。

zの根を求める際に縮約が発生します(中央の図)。aの根はaですので縮約は発生しません。結果的に、xとaを併合します。

さて、どこが作為的なのでしょうか? 実はこれ、縮約された木のランクを意図的に操作しているのです。これまで行儀のいい場合のみ図示してきましたが、蟻本の実装では縮約の際にランクを操作しません。そのため、実際には以下のようになります。

併合時に参照されるランクは根のものだけであることに注意してください。言い換えると、一回子供になってしまった頂点のランクはもう気にする必要はありません。少々乱暴ですが、縮約は根の参照の効率を改善するためだけに行われていると言ってもいいでしょう。

蟻本の例には以下のような縮約の例が掲載されています。具体的にはeをfindするとこのような縮約が発生します。

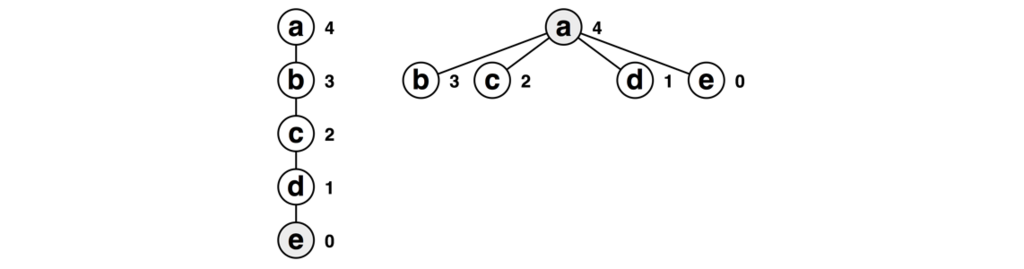
蟻本の図にはランクが示されていません。そのため、図からこのようなことが起こっていると捉えてしまっている人は少なくないかもしれません。

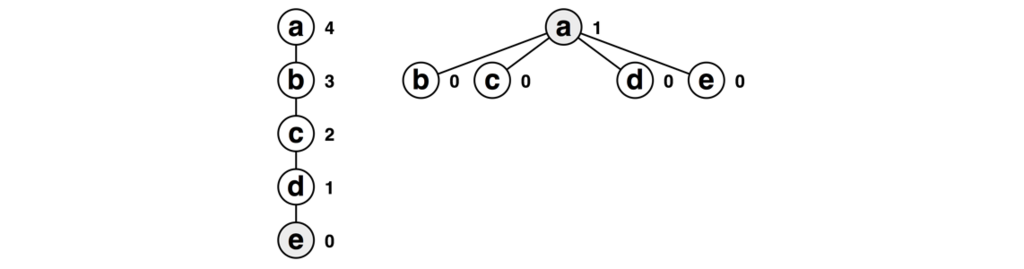
また、木の中腹の頂点をfindすると以下のような縮約が発生します。これはcをfindした例です。

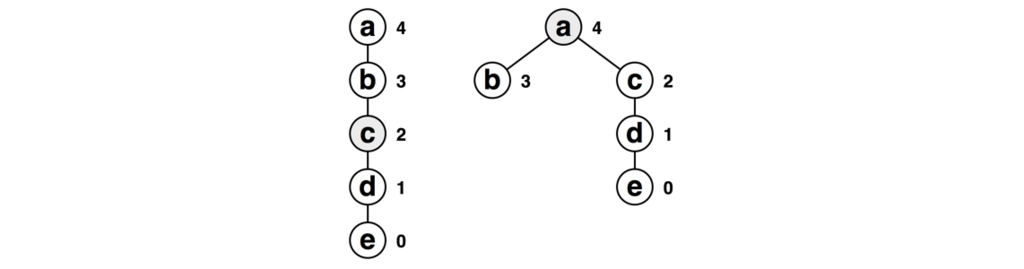
最後に、ここまでの図にはランクが2の木が出てきていました。では実際にランク2の木はどのように作ることがができるでしょう? ランクを2にするには、ランク1の木が二つないといけません(おそらく、今まで説明に使ったx、y、zの3頂点からなる木は作れないように思います)。