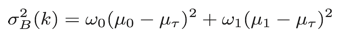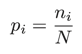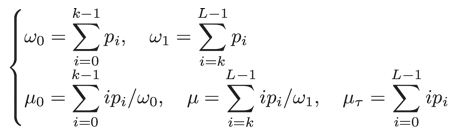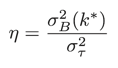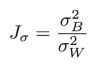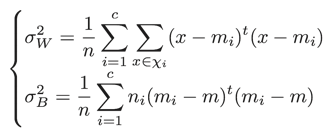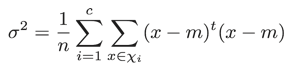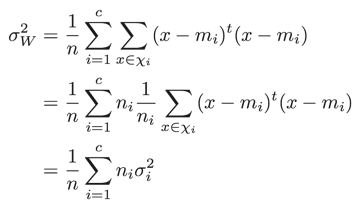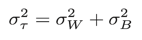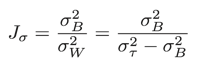To a better understanding of the Otsu’s method

大津の方法の最も有名な応用例として画像の2値化が挙げられます。この応用での圧倒的ともいえる知名度とその貢献度からか他の問題(例えば機械学習)への応用に関して明示的に言及されることが少ないですが、英語版のWikipediaの記事に記載されているように、その本質は一次元の離散な線形判別分析法の一種です(余談ですが判別分析法という呼び名の他にも判別分別法等、色々な呼び方があるようです)。

大津の方法に関しては画像解析ハンドブックのp. 1520、8 2値画像処理、8.1.2 しきい値自動決定法で詳しく紹介されています。

[2] 大津の方法
大津の判別分析法(Otsu's adaptive thresholding method)とよばれる方法であり、画像の濃淡ヒストグラムから統計的な意味での最適しきい値を決定する。あるしきい値によってヒストグラムを2つのクラスに分割した場合のクラス間分散σ_B²(k)が最大になるkをしきい値k^*に選ぶという原理である。
画像解析ハンドブック

ここで言及されているクラス間分散σ_B²(k)は以下のように計算される値です。

またNを全画素数、n_iをレベルiの画素数とします。ここからNとn_iからレベルiの画素が占める割り合いを算出することができます。これをp_iとします。

これらを元に、ω₀やω₁、μ₀やμ₁、μ_τは以下のように定義します。Lは画像全体の諧調数を表します。

これらの式を元に以下の係数ηを最大化するk^*を計算します。

右辺の分子は先に挙げた「最大化させる」式です。分母のσ_τ²は全分散です。その名の通り、全体の分散を表します。対象が画像の2値化であれば、画像全体での分散となります。全分散はしきい値にどんな値を設定しても不変なので、ηを最大化するk^*を探すときには定数として考えてしまって構いません。先ほどの抜粋では全分散に関して言及されなかったのはこのためです。

画像解析ハンドブックでの大津の方法の解説は以上ですが、これだけだと少し分かり辛いですよね。少なくとも私はそう感じ続けていました。しかし、最近わかりやすいパターン認識という書籍を読み、一気に理解を深めることができました。これを紹介したいと思います。

わかりやすいパターン認識では上述のηを変形したJ_σ、「クラス内分散・クラス間分散比」を採用し、これを「クラス間分離度」としてしきい値を評価します。

そのためにまず、「クラス内分散」と「クラス間分散」の定義をしています。以下は第5章特徴の評価とベイズ誤り確率、5.2 クラス内分散・クラス間分散比からの抜粋です。

クラスω_iに属するパターン集合をχ_iとし、χ_iに含まれるパターン数をn_i、平均ベクトルをm_iとする。また、全パターン数をn、全パターンの平均ベクトルをmとする。ここで、クラス内分散(within-class variable)をσ_W²、クラス間分散(between-class variance)をσ_B²で表す
わかりやすいパターン認識

ここで、σ_W²とσ_B²は以下とします。

続けて、わかりやすいパターン認識ではクラス内分散とクラス間分散を以下のように説明しています。

クラス内分散はクラスの平均的な広がりを表し、クラス間分散はクラス間の広がりを表している。したがってそれらの比J_σを定義すれば、J_σが大きいほど優れた特徴であると判定することができる。上記J_σはクラス内分散・クラス間分散比(within-class variance between-class variance ratio)と呼ばれる。これはクラス内距離で正規化したクラス間距離とみることもできる。
わかりやすいパターン認識

画像解析ハンドブックで解説されていた大津の方法の式と比べると

連続である
多次元のベクトルを扱っている

という差はありますが、式として圧倒的に見通しのよいものになっていることが分かります。例えばクラス内分散を算出する式は分散(全分散)を算出する式とほとんど変わず、平均値の代わりにそれぞれのクラス(ω_i)の平均値m_iとの差を取ります。逆に言えば、これに模して分散(全分散)の式を書くとすれば以下のようになるでしょう。

クラスに属するデータの分散をσ_i²とすると、以下のようにも計算できます。

クラス間分散も見た通りです。こちらはクラスに属するデータの平均値の分散を算出しています。クラスの平均値がばらつけばばらつくほど分離度が高いというのは想像と容易に合致することでしょう。

さて、J_σを一見すると、最大化するしきい値を探すときにクラス内分散とクラス間分散の双方を計算しなければならないように見えます。わかりやすいパターン認識ではその点について言及していません。しかし、全分散とクラス内分散、クラス間分散には以下の等式が成り立つことが広く知られているようです。

これを用いると、J_σを以下のように変形することができます。

分散は負の値を取りません。そのためσ_B²は[0, σ_τ²]の範囲を取ります。この区間でJ_σはσ_B²について単調増加する関数ですので、J_σを最大化するしきい値を探すにはσ_B²を考えれば十分、ということになります(σ_B²をx、σ_τ²をaとするとJ_σ = x / (a - x)であり、この微分はa / (a - x)²であることを考えてみるとよいでしょう)。