Finding Distance Between Two Nodes of a Binary Tree
yambe2002さんの記事に面白い問題が掲載されていたことをふと思い出して、考えてみました。
バイナリツリーの2ノード間の距離を求めるメソッドを作成せよ
こちらは所謂「ホワイトボードコーディング」で出題された問題だそうです。つまり、面接の問題です。
木が二分木ではない場合、ダブリングを伴ったLCAを答えることが選択肢の一つではないか、と考えました。計算量は\(O(Q\log{}N)\)です。しかし二分木であること、また電話面接だったとのことですので1、おそらく20分以内で簡潔な解法を説明することを要求されているのではないかと感じました。解法はおそらくとてもシンプルなものなのでしょう。
根の番号を1とした二分木では、頂点の番号をiとした場合に
- \(\lfloor{}i / 2\rfloor\)として親の頂点の番号を取得することができる
という性質があります。この性質をうまく使う問題ではないかと思い、考えてみました。
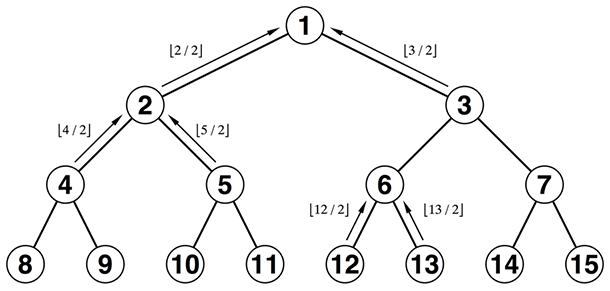
まず\(O(Q\log{}N)\)の解法をすぐ思いつきました。頂点数をN、クエリ数をQとしています。二分木なので想定して、頂点数Nはたかだか\(2^d - 1\)です(dは1以上の整数で、木の深さ)。例えば木の深さが60までだとすると、取りうるNは高々1、3、7、...、1,152,921,504,606,846,975となります。木の深さは\(\log{}N\)です。
さて、一般的な木での\(O(QN)\)の解法は以下のようなものになると思います。
- 2つの頂点の深さを合わせる(この回数を\(c_1\)回とします)
- 共通の頂点にたどり着くまで、親をたどる(この回数を\(c_2\)回とします。両方の頂点の移動量は\(2c_2\)となります)
図示すると以下のようになるでしょうか。黒い矢印が深さを合わせるフェーズで、灰色の矢印が共通の親を探すフェーズを表します。
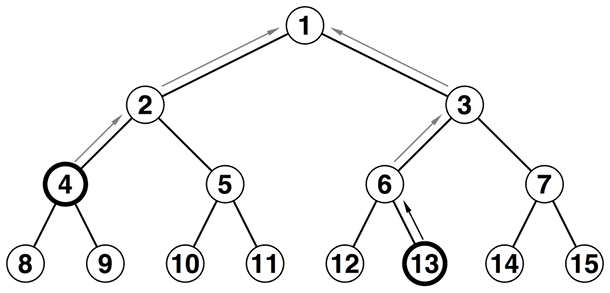
\(c_1\)と\(c_2\)から二つの頂点の距離は\(c_1 + 2c_2\)と計算することができます。
頂点の深さを求めるにはどうしたらよいでしょう? 一般的な木の場合はDFS等で事前に記録しなければならなさそうですが、こちらも完全二分木ならではの求め方がありそうです。これは各頂点の番号を二進数として表すことで規則性が見えてきました。
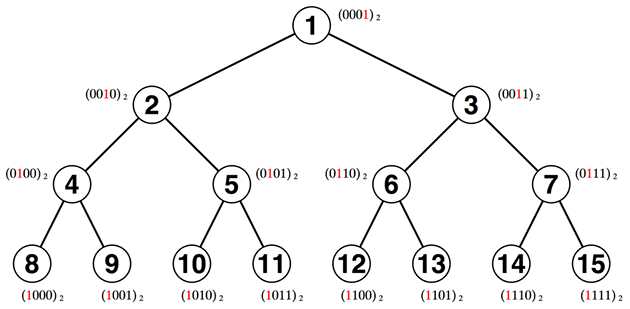
つまり、同じ深さの頂点は高位の1のビットが現れる位置が同じであるわけです。これを行うには何らかのビット演算を行う必要があるように思いました。おそらく効率のよろしくないであろう実装を書き始めることも出来そうですが、後に回すことにしました。
深さが合っていれば、共通の頂点にたどり着くまで親をさかのぼればよいです。この回数を\(c_2\)として数えます。
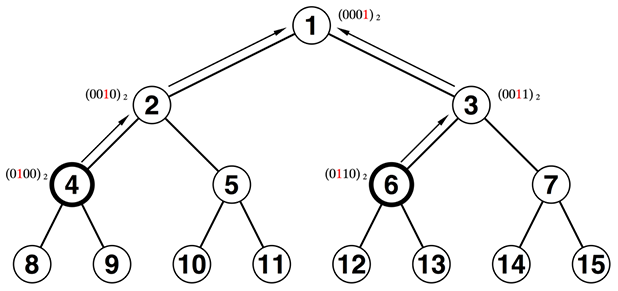
実装はおそらく以下のようなものになるのではないでしょうか(ここから全編を通して\(x \le y\)であるものとしています)。
// ゴニョゴニョした結果、xとyの深さは揃っているものとする int c2 = 0; for ( ; x != y; c2 ++, x /= 2, y /= 2) ; return c1 + c2 * 2;
これで\(O(Q\log{}N)\)の実装は完成です。
こう考えると、予め深さの調整をせずとも単純に深い方の頂点を上に持ってきてもいい気がします。
int c = 0; for ( ; x != y; c ++) (x > y ? x : y) /= 2; return c;
より簡潔に書けました。追いかけっこをしているようなので、そのように名付けます(追いかけ)。深さを合わせる実装も必要なくなってしまいました。めでたしめでたし。
...さて、時間が余ってしまいました。ここで面接官が世間話をしてくることはおそらくないでしょう。次の問題を出題するかもしれません。また、計算量を\(O(Q\log{}N)\)から下げる方法はないか検討することを求めてくるかもしれません。
ここで先ほどの図をよく眺めてみます。親の親の頂点番号は場号を右側に2つシフトしたものとなっていますね。これは利用できないでしょうか?
同様に、n個上の親の頂点の番号はx >> nで算出することができそうです。二つの頂点の深さが等しければ、ビットシフトを利用して二分探索をすることができそうです。

// ゴニョゴニョした結果、xとyの深さは揃っているものとする int l = -1, u = 66; while (u - l > 1) { int m = (l + u) / 2; ((x >> m) == (y >> m) ? u : l) = m; } return c1 + 2 * u;
この実装の計算量は\(O(Q\log\log{}N)\)となります。計測してみると、確かに速い。\(O(Q\log{}N)\)のものに比べて10倍速い結果となりました。
さて、おざなりにしていた深さを揃える実装を考えてみます。以下のように頂点の高さを揃えたいのです。
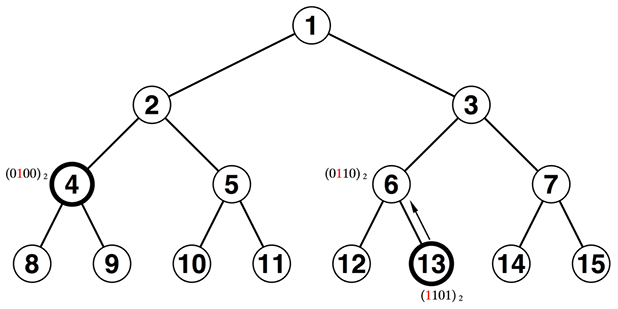
試しに書いてみたのですが、どうもどんくさい。
int c1 = 0, c2 = 0; long long s = (xのビットをゴニョゴニョする), t = (yのビットをゴニョゴニョする); for ( ; s != t; t /= 2, y /= 2, c1 ++) // 深さを揃える ; :
どうもうまく書けない。そこでnaoya_t氏にご登場願いました。この話の背景、\(O(Q\log{}N)\)、\(O(Q\log\log{}N)\)の実装アイデア、深さを揃えるところをうまく書けていない...10分ほど会話をしたでしょうか。
1時間ほど経ってnaoya_t氏から一報が届きました。実装含め、完了したとのこと。内容は目を疑うようなものでした2。
int c = __builtin_clzll(x) - __builtin_clzll(y); return c + (64 - __builtin_clzll(x ^ (y >> c))) * 2;
結局のところ、二分探索も必要なく3先頭からの0のビットの数を数えること(clz / Count Leading Zero)とビット演算だけで求めることができる、とのことでした。びっくり4。
まず双方の番号のclzを取得して、大きい方の番号をclzの差の分だけ右側にシフトします。これで深さが揃います。以下の例の場合、\(5 - 4 = 1\)ビットだけ右側にずらしてやります。
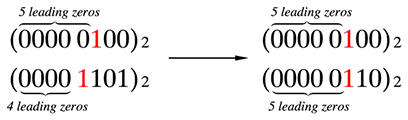
さらに、排他的論理和を取って二つの数のビットが異なる初めてのビットまでの位置をclzで取得します。このビット以降をなくしてしまえば、それは共通の祖先の頂点であると言えそうです。またその距離は右側からこのビットまでのビット数(bsr / Bit Scan Reverse)です。つまり総ビット長(実装では64、図では8)からclzを引いた分が共通の頂点までの距離となります。この距離は2倍しなければならないことに注意してください。
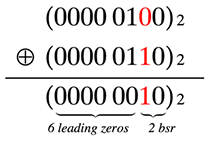
さて、計測です。\(O(Q\log\log{}N)\)のものに比べてさらに10倍速い。clzは大抵CPUで用意されているので当然と言えば当然です。clzの計算量を\(O(1)\)とすると、全体の計算量は\(O(Q)\)です。
ちょっとしたあとがき
このブログはnico_shindanninさんが主宰するCompetitive Programming Advent Calendar 2017 - Adventarの飛び込みエントリとして書いてみました。氏は多忙であるにも関わらずコミュニティのアクティビティに貢献し続けています。いつも本当にありがとうございます(就寝するときはシンガポールに足を向けないようにしています :))。遅筆なところ急ぎ書き起こしたため、読み辛い部分が多いと思います。ごめんなさい。
最近ありがたいことに人付き合いに恵まれ、コンテスト以外でのアクティビティが充実しています。と言っても、解けた問題のレビューをしたり、解けなかった問題を教わったり。競技プログラミングのみならず、オンラインコースでの勉強、英会話などなど。大変充実した時間を過ごしています。
アルゴリズムの勉強方法にも少しずつ工夫を取り入れています。あまり派手ではありませんが、レートもジワジワ上がってきていて効果を実感してきています(Codeforcesで100くらい、ですかね)。
- コンテスト終了時に取り組んでいた問題をコンテスト終了直後にリマインダーに突っ込み、復習する
- 自分が実現したい不明なテクニックがあった場合、コンテスト中でもリマインダーに突っ込む
- コンテストに参加できなかった知人に良問だと思った問題をリコメンドする(また、知人のレベルではやらなくてよい問題も伝える)
- 良問についてダラダラ語る
問題について議論することが相当効いているようです。本文にご登場いただいたnaoya_t氏の発想は自力ではなかなかたどり着けませんし、また氏曰く、自分が考えていた追いかけや二分探索の発想はまずしなかったそうです(ビット演算系がうまく行かなかった後の選択肢なんでしょう)。もちろんコンテスト終了後のTLによる感想戦でもこのような知見に出会えるのですが。コンテストからしばらく経ったあとでも議論したりしているとことがいいんでしょうか。
さて、面接で求められていたのはどの程度なんでしょうかね。気になるところではあります。題材として引用することを快諾くださったyambe2002さん、どうもありがとうございました。
ちょっとした追記
「ビットをゴニョゴニョする」のに、最高位のビットだけ残すことを考えていました。つまり、2の冪での床関数です。分岐なしで\(O(log{}N)\)の実装なので、これはこれで大変高速です(これだけ命令があってclzの倍程度)。
inline long long bfloor(long long x) { x |= x >> 1; x |= x >> 2; x |= x >> 4; x |= x >> 8; x |= x >> 16; x |= x >> 32; return x - (x >> 1); }
例えば\(0010\ 1011\)を渡すと\(0010\ 0000\)を返します。