Idiom: Getting the largest number that is less than x

プログラムを書いているとき、思ったことが思った計算量でできることは分かっているのに細かい処理がパッと書けないことってありますよね。今日はこの問題を解いているときに、「std::mapのキーがx未満で最大のものを得たい!」と考え至ったのですが、すぐに繰り出すことができず、悔しい思いをしました。

コンテスト中にこういうことが起こるのはよくあります。よくあることなのであればイディオムとしてまとめられるのではないかな、と思いました。

今回のイディオムは以下です。ただし、要素は整列されているものとします。

x未満の最大の値を得る

これはO(logN)で行うことができます。具体的には以下のようにします。

std::lower_boundでxの下限を探す。反復子が示す要素の一つ前の値が求める値である

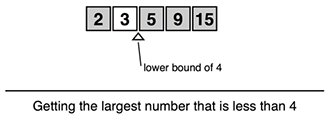
これを図で表せば以下となります。例では4未満の最大の値を探索しています。

要素群にx未満の値がない場合、std::lower_boundは先頭を指し示す反復子を返します。このとき、一つ前の要素にアクセスすることはできないので注意が必要です。

コンテナ独自のlower_boundメソッドを持つstd::setを使って観察してみましょう。std::setの内容は2、3、5、9、15とします。

std::set<int> set = {2, 3, 5, 9, 15};

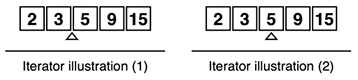
さて、STLの反復子は要素の間を指し示すものとするとすっきりと考えることができるものも多いです。ここからは以下の図の左の表現方法を取りたいと思います。

3未満の最大の値を探してみましょう。lower_boundの結果は以下のようになるため、反復子を一つ戻したものが求める値、2になります。

auto it = set.lower_bound(3);

//  set: 2 3 5 9 15
//        ^
//        `-- it

*(-- it);	// 3未満の最大の値は2

次に9未満の値を探してみましょう。

auto it = set.lower_bound(9);

//  set: 2 3 5 9 15
//            ^
//            `-- it

*(-- it);	// 9未満の最大の値は5

7のように要素として存在しない数値の場合はどうでしょうか? その場合も問題なく動作します。

auto it = set.lower_bound(7);

//  set: 2 3 5 9 15
//            ^
//            `-- it

*(-- it);	// 7未満の最大の値は5

もちろん、21のように大きな値を入れてもきちんと動作します。この場合、itはstd::end(set)を指しますが特に問題はありません。

auto it = set.lower_bound(21);

//  set: 2 3 5 9 15
//                 ^
//                 `-- it

*(-- it);	// 21未満の最大の値は15

最後に先頭の値、例えば、2未満の最大の値を探す場合ですが、これは注意が必要です。itの一つ手間の要素にアクセスすることはできないからです。

auto it = set.lower_bound(2);

//  set: 2 3 5 9 15
//      ^
//      `-- it (= std::begin(set))

*(-- it);	// これはアクセス違反!

そのため、lower_boundを試したあとに反復子が先頭にあるかどうか調べる必要があります。

auto it = set.lower_bound(x);

if (it == std::begin(set)) {
  // x未満の値は存在しない
}
else {
  *(-- it);	// x未満の最大の値
}

イディオムがはっきり見えてきました。aをコンテナとすると以下のように書くことができそうです。

auto it = std::lower_bound(std::begin(a), std::end(a), x);

// または、auto it = a.lower_bound(x)

if (it == std::begin(a)) {
  // x未満の値は存在しない
}
else {
  *(-- it);	// x未満の最大の値
}