How to Find Palindromic Substrings?

Algorithm !

回文に関連する実装が苦手です。

回文について考えなければならないときはいつも気が重かったのですが、与えられた文字列から回文となる部分文字列を列挙する方法を@nico_shindanninさんがニコニコ生放送で解説していらっしゃいました。とても分かりやすい解説だったので、メモとしてまとめました。


次の文字列を考えてみます。

例えば先頭から5文字の部分文字列、CBABCは回文になっています。同様に、どのくらいの部分文字列が回文になっているでしょう? まずナイーブなO(N3)を実装して確かめてみました。

def palindromes(s):
    size = len(s)
    for i in range(size):
        for j in range(i, size):
            l, u = i, j
            while l <= u:
                if s[l] != s[u]:
                    break
                l += 1
                u -= 1
            else:
                yield s[i:j+1]

これはとても直感的な実装です。

  • 部分文字列を列挙し
  • 回文であるかどうか

を調べています。

この実装の動作を図示すると次のようになります。回文となる文字列の数は意外と多く、9個ありました。


さて、続いては@nico_shindanninさんが紹介していた方法です。回文の性質をうまく利用して、部分文字列の中央から広げて行くようにチェックを行うことによって計算量をO(N2)に落としています。

def palindromes(s):
    size = len(s)
    for i in range(size):
        l = u = i
        while 0 <= l and u < size:
            if s[l] != s[u]:
                break
            yield s[l:u+1]
            l -= 1
            u += 1

        l, u = i, i + 1
        while 0 <= l and u < size:
            if s[l] != s[u]:
                break
            yield s[l:u+1]
            l -= 1
            u += 1

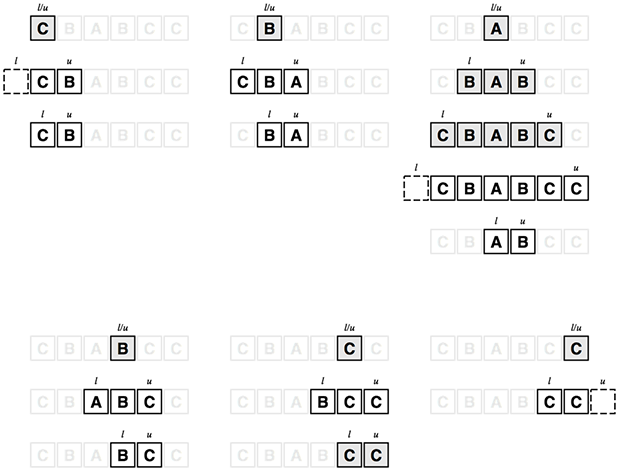
こちらの実装の動作を図示すると次のようになります。


文字列の長さが10,000個の場合、O(N2)の実装は手持ちの端末で0.1秒以内に終わりますが、O(N3)の実装では10秒ほどかかりました。

@nico_shindanninさんの放送のおかげで回文に対する苦手意識が少し和らぎました。これからは回文を使った問題も積極的に解いて行こうと思います。

Understanding How std::string::substr works

Algorithm !

STLやPythonで範囲指定の多くは左閉半開区間を基調にしています。しかし、std::string::substrでの範囲指定は大きく異なり、戸惑います。気が付くと実装時に繰り返し同じことを考え、無駄を感じていたのでまとめてみました。


以下はstring::substr - C++ Referenceからの抜粋したstd::string::substrの書式です。

string substr (size_t pos = 0, size_t len = npos) const;

string::substr - C++ Reference

冒頭で触れたように、STLでは左閉半開区間での範囲指定を基調としていますが、std::string::substrではposとlen、つまり、位置と長さで範囲を指定します。

位置は0ベースで指定します。

指定した範囲が文字列の後ろ側にはみ出してしまっても適切に処理をします。

第2引数は省略可能で、デフォルトの値はstd::string::nposです。これを用いると、文字列の最後までが処理の対象になります。

位置posは文字列の長さまで指定することができます。文字列の長さを指定したときは、空文字を返します。それ以降を指定すると例外が発生します。

文字列をある位置で2つに分割する機会はなかなか多いのではないでしょうか? 以下はその例です。この場合、前半の文字列の長さを後半の文字列の開始位置とします。

前半の開始位置が0ではない場合は以下の式を用いるとよいでしょう。後半の文字列の開始位置は前半の開始位置にその長さを足した値とします。

以下はその例です。


Effective STL―STLを効果的に使いこなす50の鉄則

Effective STL―STLを効果的に使いこなす50の鉄則

  • 作者: スコットメイヤーズ,Scott Meyers,細谷昭
  • 出版社/メーカー: ピアソンエデュケーション
  • 発売日: 2002/01
  • メディア: 単行本
  • 購入: 9人 クリック: 155回
  • この商品を含むブログ (95件) を見る

Implementing Sieve of Eratosthenes

Algorithm !

エラトステネスの櫛はN以下の素数を列挙するアルゴリズムとして知られています。まずは素数を列挙するナイーブな実装を行い、計算量を落としていきながらエラトステネスの櫛を考えてみることにします。

次の実装の計算量はO(N2)です。

#include <iostream>
#include <vector>


#define N 100000


int main(int argc, char** argv)
{
  std::vector<bool> is_prime(N + 1, true);

  is_prime[0] = is_prime[1] = false;

  for (int i = 2; i <= N; i ++)
    for (int j = 2; j < i; j ++)
        if (i % j == 0) {
          is_prime[i] = false;

          break;
        }

  return 0;
}

この実装では、

  • 2〜Nまでの全ての数iに関して、
  • 2〜i-1までの数で割り切れるかどうか

を調べています。とても遅そうです。手元の端末ではNが105のような比較的小さな値でも2秒かかりました。試しにNを106としたら終わりませんでした。


次にO(N√N)の実装をしましょう。

                  :

  for (int i = 2; i <= N; i ++)
    for (int j = 2; j * j <= i; j ++)
        if (i % j == 0) {
          is_prime[i] = false;

          break;
        }

                  :

変更したのは2行目だけです。この実装では先日のエントリで紹介した知見を利用して、

  • 2〜Nまでの全ての数iに関して、
  • iが2〜√iまでの整数で割り切れるかどうか

を調べています。

先ほどのナイーブな実装に比べるととても速く、Nが105のとき、0.15秒で終わりました。しかし、Nが106のときはまだ2.9秒ほどかかるようです。


次にエラトステネスの篩の要素を導入してみましょう。

素数の整数倍の数は素数ではありません。そのため、素数を見つける度にその整数倍の数が「素数ではない」と記録しておけば将来的にその数の素数判定をする必要がなくなるため無駄な計算が省けそうです。文字通り、探索の候補から「篩い落とす」のです。

                  :

  for (int i = 2; i <= N; i ++)
    if (is_prime[i])
      for (int j = 2; j * j <= i; j ++)
        if (i % j == 0) {
          for (int k = i; k <= N; k += i)
            is_prime[k] = false;

          break;
        }

                  :

この方法にすることによって、Nが106のときでも0.3秒で終わるようになりました。


考えてみるとこの実装にも無駄があることが分かります。

素数の倍数は予め探索から篩い落とされています。数iに訪れたときにその数がまだ「素数ではない」と判定されていなかったとすると、数iは素数である、と言えます。その数を篩うような約数がなかったからです。そのため数iが素数であるかを改めてチェックする必要もないのです。

エラトステネスの櫛の動作原理をもう少し深く理解するために作図しました(図を考えるにあたって、Sieve of Eratosthenes - Wikipedia, the free encyclopediaを参考にしました。アニメーションを使った良質な資料です。合わせてご参照ください)。

初めに2からNまでの状態を記録する領域を確保します。

まず2を処理します。2には何も記録されていません。そのため、2を素数とします。また、将来的に処理するであろう2の整数倍の数は全て素数ではありません。これを記録します。

次に3を処理します。3は2で割り切れる数ではありませんでした。そのため、3には何も記録されていません。そこで、3を素数として記録します。将来的に処理するであろう3の整数倍の数も全て素数ではありません。先ほどと同様に、これも記録しましょう。

次に4を処理しますが、4は「素数ではない」と記録されています。そのため、単純にスキップします。

次は5です。5には何も記録されていないため、素数です。3と同様の処理をします。

6からもこれを繰り返します。

説明では「記録されていない」、「素数である」、「素数ではない」の3つの状態を考えていますが、実際には「素数である」、「素数ではない」の2つの状態のみを扱えばアルゴリズムとして成立します。その場合、初めに記憶領域は全て「素数である」の状態にしておきます。

ここまでを実装に反映したものが以下です。

                  :

  for (int i = 2; i <= N; i ++)
    if (is_prime[i])
      for (int k = i + i; k <= N; k += i)
        is_prime[k] = false;

                  :

その効果は絶大で、Nが106で0.11秒で終わるようになりました。


さて、続けて7を処理した状態を考えてみましょう。

先ほどの実装では7に続き、11、13、...と処理していますが、実はその必要はありません。Nまでの素数を調べるのに2〜√Nまでを調べればよいのはエラトステネスの櫛も同様なのです。ここではNを120としていますので、√Nは10.95ほどです。そのため、10まで考えればいいことになります。

例えば120に近い113について考えてみましょう。√113は10.63です。先ほど計算した10.95よりも小さいですね。同様に、109、107、...、11までの平方根はそれぞれ11よりも小さいので、やはり高々10までを調べれば十分なのです。

今ひとつピンと来ない人には以下のように形式的に記述したもののほうが分かりやすいかもしれません。


ここまでの考察を元に、エラトステネスの篩の最終版を実装します。

                  :

  for (int i = 2; i * i <= N; i ++)
    if (is_prime[i])
      for (int k = i + i; k <= N; k += i)
        is_prime[k] = false;

                  :

WikipediaのSieve of Eratosthenesによれば計算量はO(NloglogN)だそうです。実装も随分簡素になりました。速度も速く、Nが106のときは0.006秒で終わるようになりました。Nが107であっても0.05秒ほどで終わり、108であっても0.74秒で終わります。


プログラミングコンテストチャレンジブック [第2版]　?問題解決のアルゴリズム活用力とコーディングテクニックを鍛える?

プログラミングコンテストチャレンジブック [第2版]　?問題解決のアルゴリズム活用力とコーディングテクニックを鍛える?