SRM 611 Div II

SRM 611 Div II

http://community.topcoder.com/stat?c=round_overview&er=5&rd=15844

SRM 611 Div Iに参加。戦績は惨憺たるものだった。

SRM終了後に@nico_shindanninさんのTopCoderでプログラムしてみた 第2060回(SRM611 直後放送)を視聴。そこで解説されていた素因数、最小公倍数(LCM)の解説があまりにも明瞭で素晴らしかったため、氏の許可を得てブログにまとめることにした。

さて、Div I 250とDiv II 500は類似した問題であった。Div I 250はDiv II 500の知見を利用すると効率よく解くことができる。そのため、このエントリでは生放送での解説から得られる知見を解説し、Div II 500を解くことを目標とする。

LCMSetEasy

http://community.topcoder.com/stat?c=problem_statement&pm=13040&rd=15844

  • 問題は上記のURLから参照して欲しい
    • 要約すれば、自然数xと自然数の集合Sが与えられる。そのとき、最小公倍数がxとなる集合Sの部分集合が存在するかしないかを答える問題
  • 問題について考える前にまず、約数、最大公約数、最小公倍数について考察してみよう
  • 最大公約数(GCD)や最小公倍数(LCM)を考えるときにまず与えられた数の素因数を考えるのは自然なことだ。与えられた自然数xが600であったとすると、素因数分解したものは以下となる


  • 生放送で氏はこれを以下のように図示した


  • 続いて24という数字も考えてみよう。24を素因数分解すると以下となる


  • これは以下のように図示することができる


  • さて、この数字は600を割り切る。氏の手法を用いた場合、このように図示することができる


  • ものすごく分かりやすい...次に70という数字を考えてみよう


  • 70は600を割り切らない。これは以下のように図示することができる。7がはみ出るのだ


  • 以下は18を考えた例だ。18も600を割り切らないので、はみ出る


  • 逆にいえば、はみ出る要素がなければその値は約数であると言えるし、はみ出てしまうのであれば約数ではないと言えることができる
  • 次に最大公約数を考えてみよう。計算機を使って最大公約数を求める場合はユークリッドの互除法を用いるのが一般的だが、氏の手法でも考えてみよう
  • 24と15の最大公約数を考えてみよう。これははそれぞれ、以下のように図示することができる


  • 最大公約数を考えるには重なった部分のみ抽出すればよい。論理積を取る感覚だ


  • もう一例挙げておこう。24と900の最大公約数は12だ


  • 同様に、複数の数値の最大公約数も論理積を取る感覚で考えることができる
    • 15、24、900の最大公約数は3だ


  • この図を眺めていると、複数の数値の最大公約数は以下のように考えることができることが分かる


  • また、式を以下のように変形していくと、端から数値を処理すればよいということが分かる
    • これも図からも直感的に得ることができる


  • さて、最小公倍数も同じように図示することが出来る。先ほどとは違い、論理和を取る感覚だ


  • 最小公倍数を算出する以下の式と見比べてみると楽しい


  • 複数の数値の最小公倍数も論理和を取る感覚で考えることができる
    • 例えば、24、105、900の最小公倍数は1800だ


  • 最大公約数で考えたときと同様に、複数の数値の最小公倍数は以下のように考えることが出来る


  • 式変形を行うと、最小公倍数に関しても端から数値を処理すればよいということが分かる

  • ここまでの知識をもとに、SRMの問題を解いてみよう。ある整数xと整数の集合Sが与えられるのであった。例として、xを600、集合Sの数値をS = {8, 12, 15, 18, 105, 300}とする


  • 集合Sの部分集合の最小公倍数が数値xとなるか判定するにはどうすればよいだろうか?
    • 一先ず、全ての数のLCMを取ってみよう


  • ...なんとなく600に近い形にはなっているように見えるが、3が一つ、また7がはみ出してしまっている
  • はみ出してしまうのは約数ではないからであった。なので、これらの値は除外してしまってよい。これは、値が整数xを割り切るかどうかで判断できる
  • この例の場合、18、105は除外してしまってよい


  • 改めて、はみ出さなかった数のみ、つまり約数のみの最小公倍数を考えてみよう


  • 最小公倍数の数は600となった!
  • そのため、以下の部分集合は最小公倍数がxとなるものの一つであると言える


  • 最小公倍数が600とならない場合も考えてみよう。先ほどの集合から300を抜いた場合を考えてみる


  • 先ほどと同様にはみ出す、つまり約数ではない数を除外して、最小公倍数を求めよう。その値は300となり、600には足りないことが分かる

これを実装すると以下のようになる(システムテストをパスした実装)。

class LCMSetEasy {
public:
  std::string include(std::vector<int> S, int x) {
    long long lcm = 1;

    for (const auto& i : S)
      if (x % i == 0)
        lcm = lcm * i / std::__gcd<long long>(lcm, i);

    return lcm == x ? "Possible" : "Impossible";
  };
};

まとめ

  • @nico_shindaninnさんの生放送での解説を元に約数、最大公約数、最小公倍数の図示を行い、特に複数の値の最大公約数と最小公倍数について考察した
  • この図示手法は大変簡潔で分かりやすい。最大公約数や最小公倍数を考える際、有用なアプローチの一つに成りえる
  • 氏は解説の文書化を快諾くださった。筆者の力量不足であまりよい文章に落とし込むことが出来なかったが、感謝したい

おまけ

@kojingharangさんが大変有用なつぶやきをされていたので抜粋させていただく。




Understanding How cbind/rbind works in R

Rを使うようになってきた最大の動機はR自身で柔軟にデータを作成できることにあります。例えば、パッケージユーザーのための機械学習(1)：決定木 - 銀座で働くデータサイエンティストのブログでは以下のようなXORパターンのデータを用いて決定木の解説を行っています。

「少しランダムが入った市松模様」とでもいうのでしょうか。上述のものは「シンプルなXORパターン」と称されていました。少し点群の数を増やすと市松模様を基調としている様子がはっきりしてきます。

自分も是非、こういうデータを短時間でゴリゴリ作れるようになりたいと思いました。先のエントリでは、ありがたいことにデータを作成した際のRの実装を掲載してくださっていました。

# シンプルなXORパターン
> p11<-cbind(rnorm(n=25,mean=1,sd=0.5),rnorm(n=25,mean=1,sd=0.5))
> p12<-cbind(rnorm(n=25,mean=-1,sd=0.5),rnorm(n=25,mean=1,sd=0.5))
> p13<-cbind(rnorm(n=25,mean=-1,sd=0.5),rnorm(n=25,mean=-1,sd=0.5))
> p14<-cbind(rnorm(n=25,mean=1,sd=0.5),rnorm(n=25,mean=-1,sd=0.5))
> t<-as.factor(c(rep(0,50),rep(1,50)))
> d1<-as.data.frame(cbind(rbind(p11,p13,p12,p14),t))
> names(d1)<-c("x","y","label")

...これで出来るのか、という印象。初見では何をやっているか全く検討もつきませんでした。

部分的に実行してコードリーディングを行った結果、cbindとrbindという関数が何回も登場することに気付きました。

> help(cbind)
Combine R Objects by Rows or Columns

Description:

     Take a sequence of vector, matrix or data frames arguments and
     combine by _c_olumns or _r_ows, respectively.  These are generic
     functions with methods for other R classes.

Usage:

     cbind(..., deparse.level = 1)
     rbind(..., deparse.level = 1)

                                   :

なるほど、cbindもrbindもベクトルや行列を結合する関数のようです。cとrはそれぞれ、ColumnとRowを表すとのこと。要素数の少ないベクトルや行列で実験を行った結果、なかなか一貫性のある設計であることに気付きました。


まずベクトルのcbindとrbindから考えてみることにします。ベクトルaとbを以下のように置きます。

Rでもベクトルを定義しましょう。

> a = c(1, 2, 3)
> b = c(4, 5, 6)
> a
[1] 1 2 3
> b
[1] 4 5 6

これらのベクトルをcbindしたものは行列となります。これをMcとします。Mcは以下のような、2つのベクトルを結合した行列となります。


> cbind(a, b)
     a b
[1,] 1 4
[2,] 2 5
[3,] 3 6

同様に、ベクトルをrbindしたものをMrとします。Mrの結果は以下のようになりました。


> rbind(a, b)
  [,1] [,2] [,3]
a    1    2    3
b    4    5    6

次に行列のcbind/rbindを考えてみましょう。以下のような行列SとTを考えます。

Rでも行列を定義しましょう。

> S = matrix(c(1,  4, 2,  5, 3,  6), 2, 3)
> T = matrix(c(7, 10, 8, 11, 9, 12), 2, 3)
> S
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
> T
     [,1] [,2] [,3]
[1,]    7    8    9
[2,]   10   11   12

ベクトルの場合と同様に、行列をcbindしたものをMcとします。Mcは以下のような行列となります。


> cbind(S, T)
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    1    2    3    7    8    9
[2,]    4    5    6   10   11   12

行列をrbindしたものをMrとします。Mrは以下のような行列となります。


> rbind(S, T)
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
[4,]   10   11   12

さて、どうでしょう? とても一貫していますね。引数がベクトルである場合でも行列である場合でもcbind(a, b)は以下のような行列を作成するのです。

同様にrbind(a, b)は以下のような行列を作成します。

ベクトルのcbind/rbindには少し注意が必要です - ベクトルが列ベクトルとして扱われるか行ベクトルとして扱われるかは関数によって異なります。また、cbindで以下のように合成することは出来ません(このような結合を行うにはc(a, b)とします)。


さて、ここまでのcbind/rbindの知識を元に、今一度XORパターンの実装を読んでみましょう(再掲)。

# シンプルなXORパターン
> p11<-cbind(rnorm(n=25,mean=1,sd=0.5),rnorm(n=25,mean=1,sd=0.5))
> p12<-cbind(rnorm(n=25,mean=-1,sd=0.5),rnorm(n=25,mean=1,sd=0.5))
> p13<-cbind(rnorm(n=25,mean=-1,sd=0.5),rnorm(n=25,mean=-1,sd=0.5))
> p14<-cbind(rnorm(n=25,mean=1,sd=0.5),rnorm(n=25,mean=-1,sd=0.5))
> t<-as.factor(c(rep(0,50),rep(1,50)))
> d1<-as.data.frame(cbind(rbind(p11,p13,p12,p14),t))
> names(d1)<-c("x","y","label")

さて、もう読めるようになりましたね...と簡単に行けばよいのですが、やはりまだ難解ですね。

この実装では結合した行列から最終的にデータフレームを生成していますが、行列を作成することを目標としてみましょう。as.data.frame(...)の中身を作成するところまで、と考えてください。

少し分解しましょう。まず、p11〜p14までのデータを考えてみます。これらはX座標、Y座標共に標準偏差0.5の正規分布に従ったランダムな点群です。X座標、Y座標のそれぞれのベクトルとして用意し、cbindを用いて合成をしています。以下のようなイメージです。

meanを変えることで分布の中心を変えながら、p12、p13、p14を同様に作成します。二つ目の添字が象限を表しています。例えば、p13は第三象限に分布した点群です。そのため、ほとんどの値は負の値となります。

さて、ベクトルを合成した結果は行列となるのでした。これをrbindで合成します。市松模様とするために少し工夫を施し、p11、p13、p12、p14の順番で合成しましょう。

これとは別に0と1のラベルからなるベクトルを作成します。先ほど少し触れましたが、ベクトルとベクトルを直列に合成するにはc()を用います。

最後にcbindを用いて行列とベクトルを合成します。

これで目的の行列を作成することができました。データフレームに変換しなくても行列の段階でプロットすることも可能です。

plot(M[,1:2], col=M[,3], pch=16, xlab='x', ylab='y')

まとめ


ベクトルや行列等を合成して新たな行列を作成する場合はcbind/rbindを使うと便利です。Rにはまだ慣れていないためどんな場合でもデータフレームにまとめようとする傾向にありますが、今後はcbind/rbindをどんどん活用していきたいと考えています。

もちろん好みによるとは思いますが、個人的にはmatrixを使うよりもrbindを使ったほうが直感的に行列が記述出来るよう感じています。

> S = rbind(c(1, 2, 3), c(4, 5, 6))
> S
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6

以下にmatrixを使った行列の作成を再掲します。是非比較してみてください。

> S = matrix(c(1, 4, 2, 5, 3, 6), 2, 3)

How matrix and vector are multiplied in R?

構文的な一貫性をなかなか感じられないのでRを敬遠していました。しかし時勢には敵わず、使用頻度が増えてきました。

どうせやるのであれば手が増えたほうがよいので、スニペットを多数作成し検証しています。気付いたことをブログに少しずつまとめようかと思っています。


さて、今日はvector型とmatrix型のオブジェクトの乗算を検証しました。行列とベクトルの演算は空気のように扱えないとストレスが貯まるので、どの処理系を学ぶときにも比較的早い段階で検証することにしています。

例えばベクトルの向きを調べることは重要です。vector型が列ベクトルとして解釈されるのであるか、行ベクトルとして解釈されるかで話は大きく違ってきます。

具体例を挙げてみましょう。3 × 3の行列をM、要素数3のベクトルをvとします。行列Mとベクトルvを乗じたとき、ベクトルが列ベクトルであれば、結果も列ベクトルになります。列ベクトルは行列の右側からかけます。

この演算方法を基調とする処理系をPre-multiplyな処理系などと呼びます。右辺がベクトルであることを簡潔に示すためにv'を導入しました。v'は以下のように計算されます。

これに対しベクトルが行ベクトルであれば行列の左側からかけないといけませんし、結果も行ベクトルになります。

この演算方法を基調としている処理系をPost-multiplyな処理系と呼びます。v'の要素は以下のように計算します。そのまま記述すると水平方向に長くなってしまうため右辺のベクトルを転置していることに注意してください。

Pre-multiplyな処理系とPost-multiplyな処理系で同様の結果を得るにはベクトルの方向だけでなく、行列を転置しなければいけないことに注意してください。

例えば同時座標系での移動行列を考えてみましょう。簡単に、移動行列とはあるベクトルの要素を平行移動する行列である、と考えてください。まずPre-multiplyな処理系での移動行列を考えてみることにします。

この行列は二次元ベクトル(x, y)を(Tx, Ty)だけ平行移動します。

さて、移動行列を適用することによって(x, y)が(x + Tx, y + Ty)に射影されました。これをPost-multiplyな処理系でもやってみましょう。Post-multiplyな処理系では行ベクトルを用いますが、要素の結果は等しくならなければなりません。

試しにPre-multiplyな処理系の移動行列をPost-multiplyな処理系で使ってみましょう。

何かめちゃくちゃなことになってしまいました。Pre-multiplyな処理系の行列をPost-multiplyな処理系で用いるには転置をしなければならなかったのです。

今回はうまくいっているようですね。つまり、Post-multiplyな処理系での移動行列は以下のようなものなのでした。Pre-multiplyな処理系のものと見比べて転置されていることを確認するのもよいでしょう。

ここまでで書いたように、処理系でベクトルが列ベクトルで扱われるか行ベクトルで扱われるかで行列の意味合いが全く異ります。そのため、ベクトルが列ベクトルなのか行ベクトルなのか予め調べておくことはとても重要です。言葉を変えれば、処理系でベクトルが列ベクトルで扱われるか行ベクトルで扱われるかを調べることによって、その処理系がPre-multiplyを基調として処理系かPost-multiplyを基調とした処理系かを見極めることができます。


さて、Rのvector型オブジェクトは以下のように記述します。

> v <- c(1, 2, 3)
> v
[1] 1 2 3

同様に、Rのmatrix型オブジェクトは以下のように記述します。

> M <- matrix(c(1, 0, 0, 0, 1, 0, 3, 5, 1), 3, 3)
> M
     [,1] [,2] [,3]
[1,]    1    0    3
[2,]    0    1    5
[3,]    0    0    1

Rはvector型とmatrix型の*演算子による乗算を許していますが、これは望む乗算ではありませんでした。調べてみたところ、%*%演算子を使えば望む行列ベクトル演算をするようです。早速やってみましょう。Rの処理系はPre-multiplyな処理系であると仮定し、(x, y) = (0, 0)を(Tx, Ty) = (3, 5)で移動してみましょう。

> M
     [,1] [,2] [,3]
[1,]    1    0    3
[2,]    0    1    5
[3,]    0    0    1
> v
[1] 0 0 1
> M %*% v
     [,1]
[1,]    3
[2,]    5
[3,]    1

数式で表すと以下のようになります。

さて、うまく移動出来たようですね。どうやらRの行列は列ベクトルを基調としていると言えそうです。また、戻り値がmatrix型であることにも注意しましょう。

念のため、Post-multiplyな処理系での演算も試してみましょう。数式で表すと以下です。


> M <- t(M)
> M
     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    1    0
[3,]    3    5    1
> v %*% M
     [,1] [,2] [,3]
[1,]    3    5    1

驚くことに、これもPost-multiply系であるかのように動作してしまいました。この結果から考えるに、Rで行列ベクトル演算を行う際、ベクトルは以下のように扱われることが分かります。

  • 行列 %*% ベクトル
    • ベクトルは列ベクトルであると解釈される
  • ベクトル %*% 行列
    • ベクトルは行ベクトルであると解釈される

とても柔軟な処理であるようにも見えますが少し注意が必要だな、と改めて感じました。

まとめ

  • 行列とベクトルの乗算を行うには%*%演算子を用いる
  • Rでのベクトルは文脈によって行ベクトルとも列ベクトルとも扱われる
  • RはPre-multiply前提の処理系でもPost-multiply前提の処理系でもなさそうだ

ベクトルの向きは、例えばLaTeXでベクトルを記述する際にも影響します。結果の通りRの処理系は予想以上に柔軟であり決定打には欠けますが、今後ベクトルをLaTeXで表記するときは列ベクトルを基調とし、行列演算はPre-multiplyな処理系を前提にしようと考えています。その理由はmatrixオブジェクトを生成するのに列ベクトルを並べるように要素を記述しなければならなかったことにあります。もっとも、Rの言語全体の一貫性のなさはよく話題になるようですので、最終的には列ベクトル + Pre-multiplyな処理系であるように考えるのが好みであることも少なからず影響しています。

How to Find Palindromic Substrings?

Algorithm !

回文に関連する実装が苦手です。

回文について考えなければならないときはいつも気が重かったのですが、与えられた文字列から回文となる部分文字列を列挙する方法を@nico_shindanninさんがニコニコ生放送で解説していらっしゃいました。とても分かりやすい解説だったので、メモとしてまとめました。


次の文字列を考えてみます。

例えば先頭から5文字の部分文字列、CBABCは回文になっています。同様に、どのくらいの部分文字列が回文になっているでしょう? まずナイーブなO(N3)を実装して確かめてみました。

def palindromes(s):
    size = len(s)
    for i in range(size):
        for j in range(i, size):
            l, u = i, j
            while l <= u:
                if s[l] != s[u]:
                    break
                l += 1
                u -= 1
            else:
                yield s[i:j+1]

これはとても直感的な実装です。

  • 部分文字列を列挙し
  • 回文であるかどうか

を調べています。

この実装の動作を図示すると次のようになります。回文となる文字列の数は意外と多く、9個ありました。


さて、続いては@nico_shindanninさんが紹介していた方法です。回文の性質をうまく利用して、部分文字列の中央から広げて行くようにチェックを行うことによって計算量をO(N2)に落としています。

def palindromes(s):
    size = len(s)
    for i in range(size):
        l = u = i
        while 0 <= l and u < size:
            if s[l] != s[u]:
                break
            yield s[l:u+1]
            l -= 1
            u += 1

        l, u = i, i + 1
        while 0 <= l and u < size:
            if s[l] != s[u]:
                break
            yield s[l:u+1]
            l -= 1
            u += 1

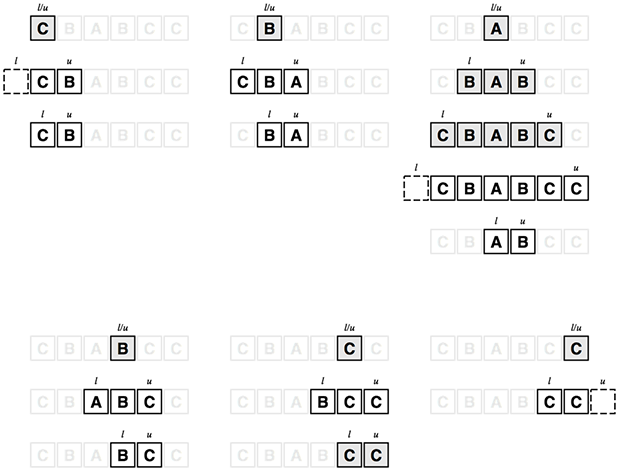
こちらの実装の動作を図示すると次のようになります。


文字列の長さが10,000個の場合、O(N2)の実装は手持ちの端末で0.1秒以内に終わりますが、O(N3)の実装では10秒ほどかかりました。

@nico_shindanninさんの放送のおかげで回文に対する苦手意識が少し和らぎました。これからは回文を使った問題も積極的に解いて行こうと思います。