How To Defeat the Opponent
How To Defeat the Opponent
- 競技プログラミングのコンテストではゲームを模した様々な問題が出題される
- 問題の解法は様々だ
- シミュレーションによる解法
- 探索による解法
- グラフの問題に還元する解法
- コンテスト終了後によく話題になる、確率DP、期待値DPなども解を探索する問題であることが多い
- このエントリでは特に解を探索する解法について、ゲームを題材とした初歩的な問題を紹介する
- ゲームを題材とした問題で頻出される「お互いが最善を尽くす」ということについて少し掘り下げて考えるとともに、探索の計算量を減らす方法を紹介する
- 紹介する問題はSRM 575 Div II 500 TheNumberGameDivTwoだ
- 対象はTopCoderのDiv II中堅〜上位を想像していただければよいと思われる
TheNumberGameDivTwo
- この問題はSRM 575 Div IIのMedium問題として出題された
- 同じ問題がDiv IのEasy問題としても出題されたが、その制約の大きさから解法は探索ではなく規則性を利用したものとなっている
- ゲームのルールは以下だ
- ある数値がある。これをnとする(n ∈ [1, 1000])
- プレイヤーは2人(JohnとBrus)
- プレイヤーは交互に数値の変更を試みる
- 新しい数値は「nからnの約数を引いた値」とする。ただし、1とnを使ってはいけない
- 数値を変更できなかったプレイヤーは負ける
- また、プレイヤー2人がお互い最善を尽くすことを前提としていることを注意すべき点として挙げておこう(原文では"Assume that both players use the optimal strategy while playing the game."としている)
- ゲームを進行した例は以下のようなものだ
- nを15とする
- Johnは15から約数の3を選んで引く。数値は12となる
- Brusは12から約数の4を選んで引く。数値は8となる
- Johnは8から約数の2を選んで引く。数値は6となる
- Brusは6から約数の3を選んで引く。数値は3となる
- 3の約数は1と3であるが、ルールによりこの値は引けない。そのため、Johnの負けと判定される
- さて、コンテスト中は限られた時間で問題を把握し、解法の方針を立て、実装、テストを行わなければならない
- ノートなどに問題のポイントや制約を記載する方は多いのではないだろうか
- その際、nに小さな(もしくは全体像を把握するのに都合がよい)値を選んで木やグラフなどをノートに書き出すといった手法を取る人は多いと思う
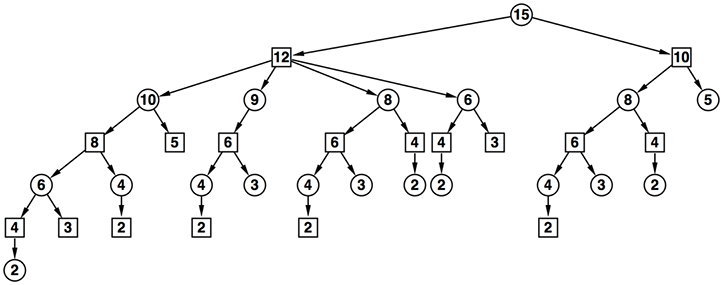
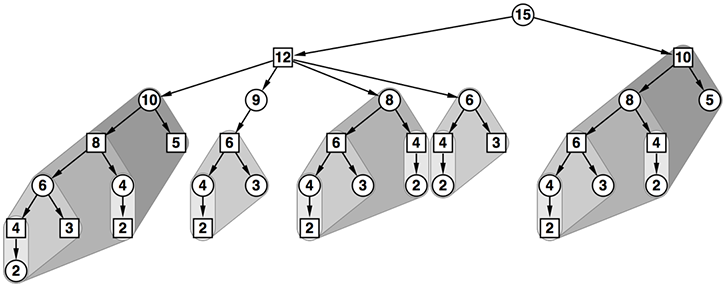
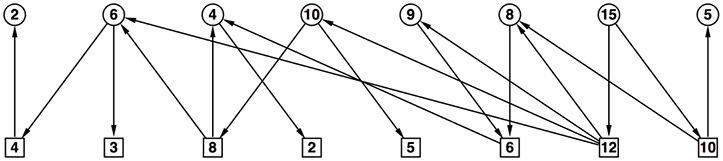
- 作図をしてこの問題の特徴を考えてみよう
- 問題文に記載されており、明らかである特徴を図に盛り込んだ
- プレイヤーは2人。交互にプレーする
- 木を描く際に先手(John)の手盤を円型の頂点で、また後手(Brus)の手盤を四角の頂点で示した
- また、図にすることによって問題文にはっきりと書いていない特徴にも気付くだろう
- 例えば次の手が同じ手になることはないことに気付く
- 期待値DPなどは解法の導出途中に同一の状態が無限に続くような探索木を考えなければいけない場合がある。何らかの変形が必要となるが、この問題ではこれを考慮に入れる必要がないということが分かる
- 他にも木は入力の数値の値が与える印象より大きくなりそうなこと、木は似通った部分木で構成されているようであることなどが挙げられるだろう
- 先に挙げた例は以下のような経路を取る
- このように問題文そのものに正解までの道筋の例が記載されているものもある
- さて、このように全体図を描くとゲームの流れを初めから追って行きたくなるが、それはあまり得策ではない
- この規模の木でも、人間が正確に状態を追うことは難しいのだ
- 実際にルールに従って15の頂点から追い、勝負の行方を考えてみるのもよいだろう(n = 15のゲームは必ず先手の負けとなるゲームである)
- 人間がゲーム木を正確に追うことを困難にさせている原因はいくつかある。このように2人のプレイヤーが交互に進めるゲームの場合、手盤によって求める答えや利益が入れ替わるのも一因となるだろう(意味合いが交互に反転しているだけにも関わらずこの有様である)
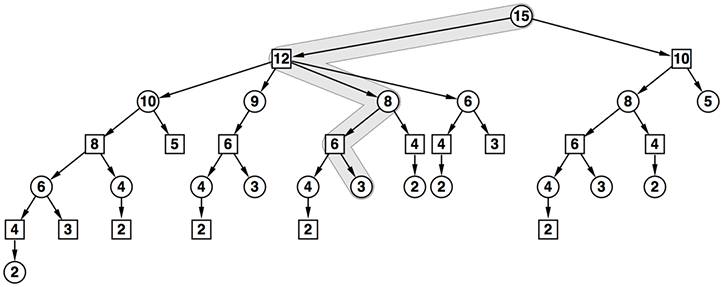
- 例を挙げよう。以下の進行では最善が尽くされていない(先手がゲームに勝っていることにも注意)。これは何故かすぐ答えられるであろうか?
- 後手は6の頂点で3の頂点に進むべきであるところを4の頂点に進んでしまっている。これは最善ではない
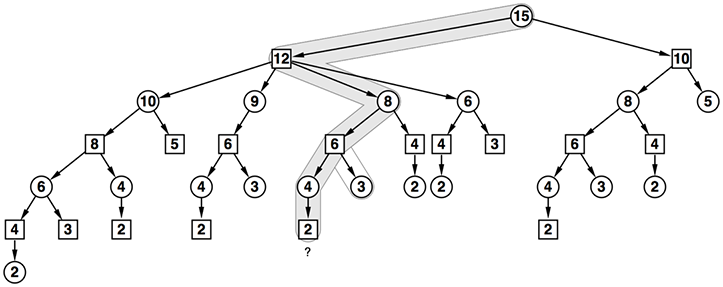
- もう一つ例を挙げよう。以下の進行でも最善が尽くされていない
- 最善が尽くされていない理由を説明できるだろうか?(情けないことに筆者には説明できない)
- 探すのみならず、結果が最善を尽くされていないことを判断するだけでも困難なことが分かる
- さて、計算機に効率よく勝敗を判定させるにはどうすればよいだろうか
- 答えは簡単だ。それぞれの頂点(局面)で最善手を選べばよいのだ
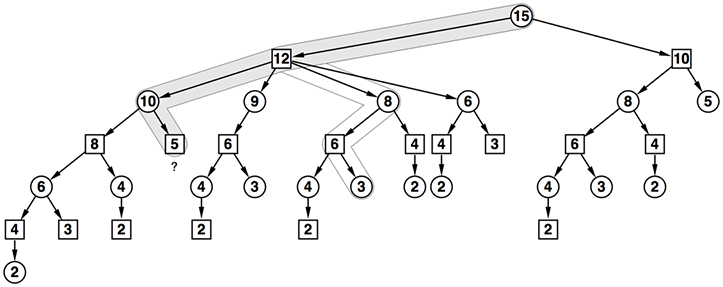
- 15の頂点は先手(John)の手盤を表している。先手は12の頂点を選ぶべきだろうか、それとも10の頂点を選ぶべきであろうか? 選ぶべき頂点をどのように予想したらよいであろうか?
- 実際に予想することはとても難しい。また、探索すべき頂点数は深さによって指数的に増えるので全探索するのは不可能だ
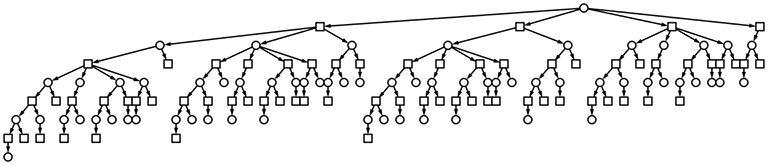
- nが大きくなるにつれ木は大きくなる。その大きくなる様は想像以上に急だ。例えばn = 18の木は以下となる(視認できないため数値を省略する - 18の頂点は16、15、12、9を頂点とする木を含むことに注意しよう)
- ナイーブな方法では解けなさそうなことは分かった
- しかしこれは競技プログラミングの問題だ
- 競技プログラミングで出題される問題の最大の特徴は出題者によって注意深くルールや制約、取りうる状態の総量が設計されていることが挙げられる。そのため、計算方法を工夫することによって解くことが可能となるような問題も多い
- この問題の場合も、計算方法を工夫することによって全ての状態を探索することが可能となる
- 全ての状態を知ることが出来るのであれば、最善手を予想するといったアプローチを取る必要はない。全ての出しうる手を計算させてしまってから最善手を選べばよいのだ。
- では先ほどの疑問に戻って考えてみよう
- 15の頂点は先手(John)の手盤を表す。先手は12の頂点を選ぶべきだろうか、それとも10の頂点を選ぶべきであろうか?
- どちらの頂点が先手にとって有利か分からなければ選びようがない
- ならば、頂点12を根とする部分木と頂点10を根とする部分木を同様の、また別の小さな問題として解いてしまえばよい
- そして、どちらの頂点が先手にとって有利か明らかになった後で選べば間違いがない
- 12の頂点を選ぶと自分が勝つのであればそれを選べばよいし、10の頂点を選んでも勝てるのであればもちろんそれを選んで構わない
- 部分木からなるゲームの結果はもう計算させてしまっているので、迷いもためらいもなく選ぶことができる
- また、何れの頂点を選んでも自分が勝つことがないのであれば、その局面でどんな手を施しても相手が勝つと断言できる
- では12の頂点を根とする部分木はどう考えればよいだろう?
- 先ほど15の頂点を考えたときと同じ問題であるが、問題の規模(この場合は数値)が小さくなっていることに注意しよう
- 問題の根本的な難しさは15の頂点を根とする場合と変わらない。ゲームの展開を予想するのは本当に難しい
- ではどうすればよいか?
- 答えは明瞭だ。先ほどと同様、小さな部分木に分割しそれぞれ計算させ、結果が出てから改めて自分に有利な手を判断すればよいのだ
- さて、これを繰り返すと末端の少しの頂点からなる部分問題とすることができる
- 頂点が一つからなる木を考えてもあまり意味がない(すぐに負けてしまうのは明らかだ)ので、頂点数が最低でも2つの木を考えてみる
- 4の頂点を根とする部分木はそのような小さな部分木である
- 観察すると2種類あることが分かる
- 先手から始めているか、後手から始めているか
- ここでは同様に処理をすることにする
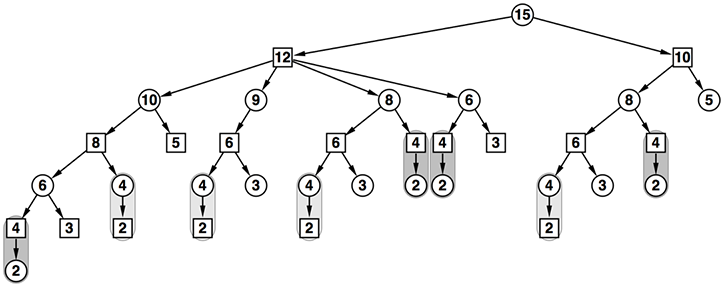
- これらの部分木の勝負の行方を考えてみよう。先手が勝つ部分木は薄い灰色で、後手が勝つ部分木は濃い灰色で塗り分けてやる
- この結果を使って、6を頂点とする部分木の勝負の行方を考えてみよう
- 6の頂点の勝敗はその子供の4か3の頂点からなる部分木の結果から得ることが出来る
- 一番左の部分木で考える。この部分木の根、つまり6の頂点が先手番であることに注意すると、
- 4を頂点とする後手からの部分木では先手が負ける
- 3を頂点とする後手からの部分木では後手の選択肢がない。先手が勝つ
- ことが言えるので、先手は3を頂点とする部分木の勝負の結果を迷わず採用するべきである
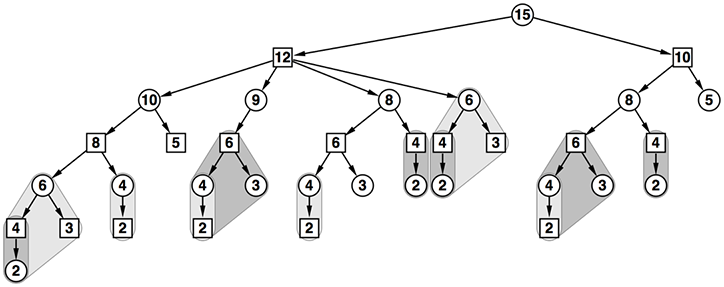
- これを反映すると、以下となる。
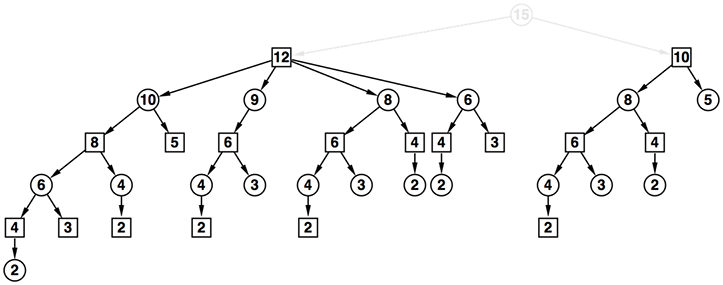
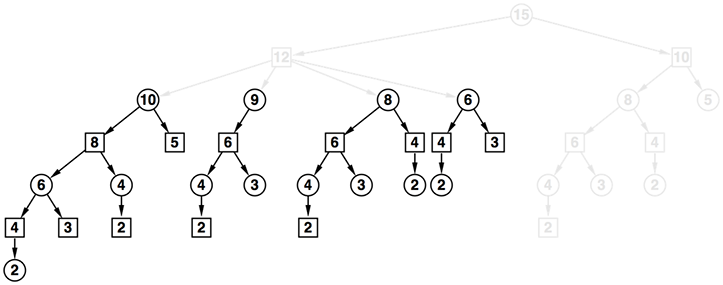
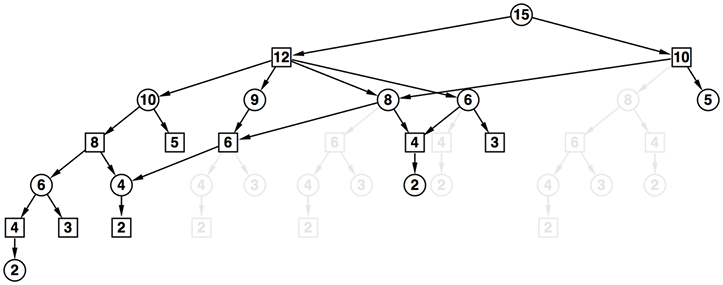
- これを繰り返していく。12を根とする部分木と10を根とする部分木は以下のように調べることが出来た
- では改めて12の頂点を根とする部分木を考えよう
- 根は後手番であるので、後手が勝つ頂点9もしくは8を選べばよい
- とても簡単
- 全ての部分木の試行を行い、自分の利益を最大化する手を選ぶ
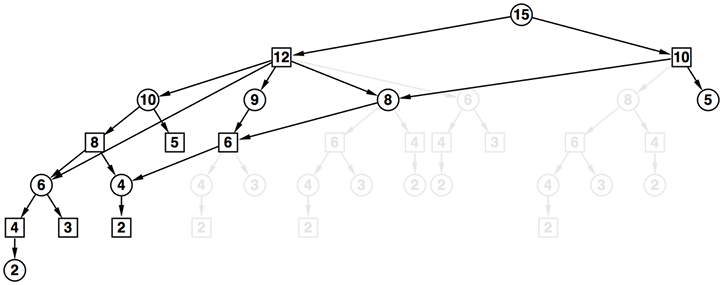
- 特にこの問題では部分木の結果が自分にとって有利な結果である場合、すぐに探索を打ち切ることができる
- 「最善を尽くしている」ということは、「勝てる手があるのであれば、迷わずその手を選ぶ」ということであるため、探索を続行する必要がないと考えてもよい
- 12の頂点を根とする部分木問題の結果は15の頂点、つまり先手に対して不利な手であることが分かったため、これを選ぶことはできない
- 同様に15の頂点の右側に位置する10の頂点を根とする部分木問題でも後手が勝っている。そのため15の頂点で先手が勝てることはないのだ
- 結果、n = 15の場合は後手が勝つのであった
- さて、以上が「勝てる手を予想する」のではなく「手を次から次へと試す手法」の解説であった
- ここからは計算量とメモリ使用量を落とす方法を考えてみよう
- 前述したが、この探索木は数値が大きくなるにつれ指数的に大きいものとなっていく
- 以下はn = 18のときの木の規模を図にしたものだ(再掲)
- この計算量を落とすのに、「メモ化再帰」「動的計画法(DPテーブル)」という技法を使おう
- DPに関しては本年のCompetitive Programming Advent Calendar Div2013にて@nico_shindanninさんが「動的計画法が苦手な人が、動的計画法が超苦手な人へアドバイスしてみる」として寄稿してくださる予定である(12/8予定)。是非合わせてお読みいただきたい
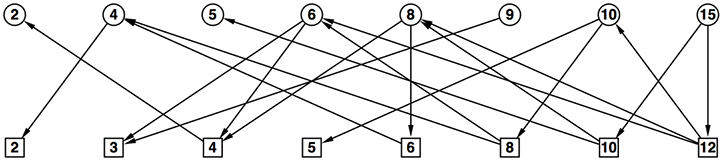
- さて、n = 15の木をもう一度眺めてみよう(再掲)
- 同じ数値の頂点が頻出していることが分かる
- 同様に、同じような部分木も頻出している
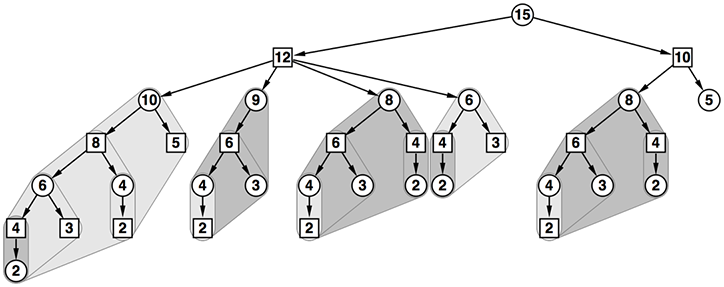
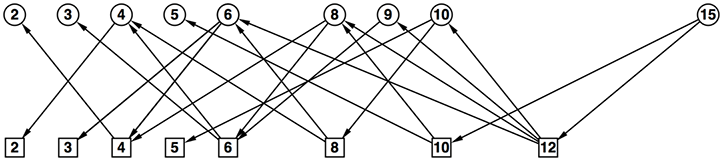
- 厳密には先手が始める部分木か後手が始める部分木かで結果が違う(反転する)が、同じような計算として括り出してみよう(彩色の意味合いが先ほどと異なることに注意)
- 例えば、8の頂点を根とする部分木は3箇所ある
- これらの計算結果は同じものとなるはずだ
- そのため、計算した結果を記録しておき、後で使うことで重複した(無駄な)計算を省略することができるはずだ
- 計算方法を省略するこの方法はメモ化などと呼ばれている
- この図は(深さ、数値)のペアを鍵として結果を記録している
- 正確な木の深さは計算をしてみないと分からないのだけれども、与えられたnがずっと2で割れる数値に変換されると無理矢理仮定したとして、高々500程度だろう
- 深さが500ほど。また、数値は1,000種類あるので、500,000個ほどの数値が記録できればこの問題は十分に解ける
- また、数値nの約数の数は高々n/2であることも容易に想像ができる
- n = 1,000の場合でも500個の約数を試せばよい
- そのため計算量も500,000 × 500 = 250,000,000
- 十分間に合う
- この問題ではもう少し工夫が出来る
- (深さ、数値)ではなく、(先手番か後手番か、数値)のペアを鍵として結果を記録してみよう
- 木で表すと以下のようになる
- 先ほどの図と比べると、さらに計算すべき頂点の量が減っていることが分かる
- 先手番か後手番かは2種類。また、数値は1,000ほどであるので、2,000個ほどの数値が記録できれば十分となった
- 先ほどと同様に計算量を見積もると、2,000 × 500 = 1,000,000
- さらに掘り下げて考えてみる
- 先手番の次は必ず後手番であることを考えると、さらに計算量を減らせることが分かる
- 先手番の手として計算しなければいけない頂点に重複がないことに気付いたであろうか
- 同じことが後手番にもいえる
- これを利用してみよう
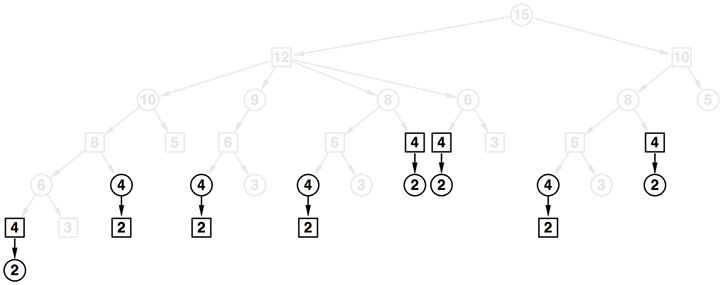
- まずさきほどの探索木の垂直方向の配置を変えてみよう
- 計算する必要がない要素を省き、揃えてみよう
- 随分シンプルな図となってきたが、今ひとつ一貫性がない
- 水平方向の並びを、数値の大きさで整列してみよう
- これも今ひとつ
- では、水平方向の頂点の位置を数値の大きさと比例するようにしてみよう
- 先手と後手の数値の対応が明確になったと共に対象性も見えてきた
- さてここで、特にプレイヤーが2人のゲームに顕著に表れる特性を利用しよう
- 先手がある数値nからゲームを始めて勝ったとしよう。後手がその数値nからゲームを始めると当然後手が勝つ
- つまり、対象性があるのだ
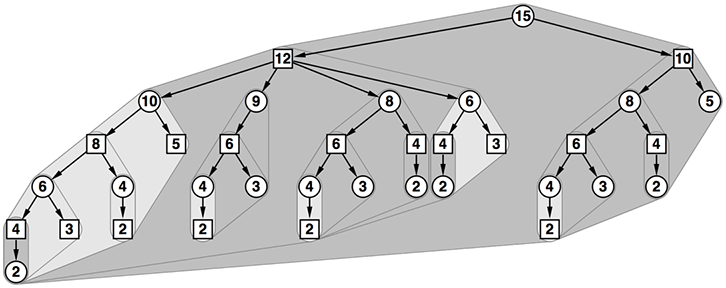
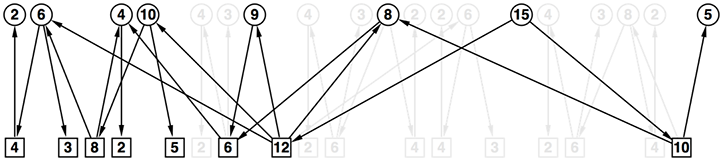
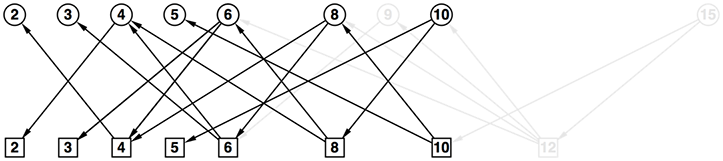
- 先ほどの図からいくつかの要素を取ると、よりはっきりと対象性が見えてくる
- 図から先手番、後手番という概念をなくすと以下のようになる
- (先手番か後手番か、数値)ではなく、ただ単に数字を鍵として結果を記録することが出来るようになってしまった
- これは一次元のDP配列を用いた動的計画法、などと呼ばれる
- メモリ使用量は数値の数だけ、つまり1,000個ほどで済むようになった
- 計算量は1,000 × 500 = 500,000
- メモリ使用量、計算量が減ったとともに、図としてもすっきりしたものとなった
- ここまで読んでいただいてどうもありがとうございました
まとめ
- 今回はCompetitive Programming Advent Calendar Div2013に向けた特別な記事ということで、ゲームを題材とした初歩的な問題の紹介を試みた
- (恐らく)赤コーダー、黄コーダーは問題を読み終えた段階で最後の図が頭に浮かんで来ているのではないかと考える
- そのため、上位コーダーはこの問題を5〜7分程度で提出する
- さてゲームを題材とした問題は頻出するが、それぞれ独特の癖があるので苦手意識を持っている人は多いと思う
- しかし、解法にはある一定のパターンもあるようだし、コツを掴むことによってAC率が上がるのは間違いない
Competitive Programming Advent Calendar 2013について
- 本日はCompetitive Programming Advent Calendar Div2013の1日目ということで、Binary2D(@Respect2D)さんが素晴らしい記事を寄稿なされている。是非ご一読いただきたいと思う
- また、明日はnodchip@C85火曜日西す03b(nodchip)さんとkomiya(kou_miyam)さんが寄稿される。明日もお楽しみに!