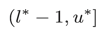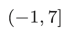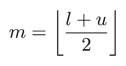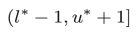二分探索で失敗しないために

二分探索で失敗しないために

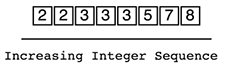
範囲を求める整数の二分探索を書いていると混乱するときってありますよね。でも全然書けないわけじゃないんです。すっきり書けることも多い。でも、こういうことがよく起こるんです。

• 無限ループに陥る
• 範囲を狭めるとき、下限と上限の何れを更新してよいか迷う
• 答えが一個ずれている

ごく最近幾つかのコツを掴んでようやく迷わず書けるようになってきました。今後も二分探索で失敗しないためにまとめてみることにしました。

探索の型を見極める

範囲を求める整数の二分探索は大きく2つに分けることができます。これを設計段階で見極めておくことが重要であるようです。

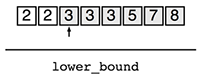
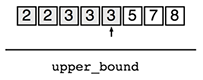
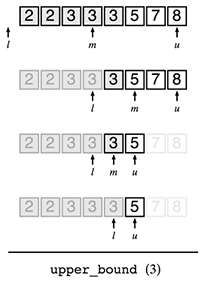
本エントリではそれぞれの型をlower_bound型、upper_bound型と呼びます。C++のSTLで実装されているstd::lower_boundとstd::upper_boundを参考としました。日本語にすれば、下界型(下限型)、上界型(上限型)とでも言うのでしょうか。

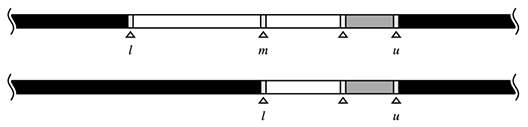
灰色で図示されている要素は「i番目の要素をa_iとしたとき、関数f(a_i)が真である」ことを表しています。下限と上限は楔(くさび)で表しています。テキストエディタで言えば、「文字と文字の間にカーソルがある」ような位置の考え方です(余談ですが、実際にテキストエディタを設計する場合はこのような位置の考え方をすると設計が簡潔になるそうです)。

続いて、位置が要素の位置にある考え方も図示します。

上の楔型と要素型の図示の間には不整合性がありますが、後で明らかになりますので今は放っておきましょう。

文章でも言い表しておきましょう。

• lower_bound型
  • 関数f(a_i)が真となる最小のiを探索する
• upper_bound型
  • 関数f(a_i)が真となる最大のiを探索する

また、二分探索はその性質上、以下のようなデータには適用できません。

関数f(x)ってなに?

まずは簡単な例で考えてみましょう。整列済みの数値の配列を例にします。

lower_bound型としては以下のような問題を考えます。

a_iが3以上である最小のiを求める

図示すると以下となります。0-indexで考えたとき、2が解となります。

このとき、関数f(x)は以下のような関数となります。

bool f(int x)
{
  return x >= 3;
}

upper_bound型としては次のような問題を考えます。

a_iが3以下である最大のiを求める

図示すると以下となります。0-indexで考えたとき、5が解となります。

このとき、関数f(x)は以下のような関数となります。

bool f(int x)
{
  return x <= 3;
}

初期範囲を決める

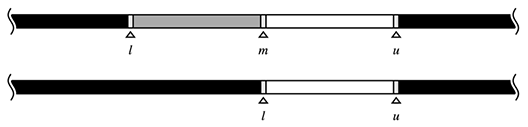
求める解の範囲が分かっている場合、言い換えれば、ある範囲の中に必ずf(a_i)が真となるiがある場合は以下のような範囲を用います。ここで、l^*とu^*はそれぞれ解が取りうる範囲の下限と上限を示します。

図示すると以下のようになります。

範囲を扱う際は右閉半開区間を用います。例えば、i ∈ [0, 7]の範囲に解があることが分かっているのであれば、初期の範囲を(-1, 7]とします。

C++の実装で表すと次のような感じになります。

  int l = -1, u = 7;

右閉半開区間を用いるのは計算機の整数演算を巧みに利用するためで、以下のような特徴があります。

• 無限ループに陥らない
• 同じ要素が複数回評価されることがない

反復の条件

二分探索は範囲をしぼり込むことによって探索を行います。範囲から要素がなくなってしまっては意味がありませんのでその直前で反復を停止します。具体的には範囲がただ一つの整数値を表している場合、つまり範囲が(x - 1, x]となったら反復を終了します。C++での実装は以下のようになります。

  while (u - l > 1) {
          :
  }

後でまた触れますが、このように実装したときにf(l^* - 1)やf(u^*)が評価されることはありません。

範囲を更新する

二分探索は反復毎に範囲を約半分に狭めていくことによってO(logN)の計算量を実現しています。各反復ではまず中央の値を計算します。整数演算ですので、端数は切り落とされます。

中央の値を使い、f(a_m)を評価します。その結果によって範囲を更新します。

• mでuを更新する(更新した範囲は(l, m]となる)
• mでlを更新する(更新した範囲は(m, u]となる)

さて、この節では一先ず細かいことを抜きにしてどのように範囲の更新を行うかを注視したいと思います。そのため、要素を詳細に記した図は一度お休みし、より概念的な図を用いることとします。

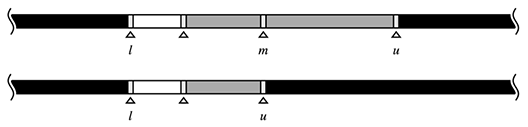
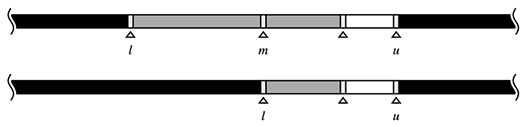
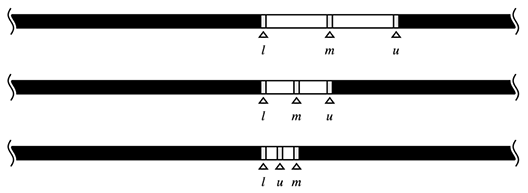
範囲を更新する際は、それが全体の範囲のどこにあるか、どの程度の大きさであるか等は意識しないほうがいいです。そのため、左右を切った図とします。lとuに挟まれている区間が注目している区間です(以下の図はuppper_bound型)。

また、更新する範囲は探索の型で異なります。lower_bound型から説明します。

lower_bound型における範囲の更新

• lower_bound型であり、現在注目しているf(a_m)が真である場合

mは解かもしれませんが、f(a_i)が真となる要素iはmよりも左側にまだあるかもしれません。ですので、左側をさらに詳しく探索します。

もちろん次の図のように、中央の値が求める解である場合もありますが、二分探索の途中でこれを意識する必要はありません。また、むしろ意識しないほうがよいようです。慣れてくると、放っておいてもアルゴリズムがこの解を絞り込んだ範囲に放り込んでくれることが分かってくるからです。

• lower_bound型であり、現在注目しているf(a_m)が偽である場合

求める解はmよりも右側にあります。ですので、右側をさらに詳しく探索します。

C++で実装すると以下のようになります。

  if (f(m)) {
    u = m;
  }
  else {
    l = m;
  }

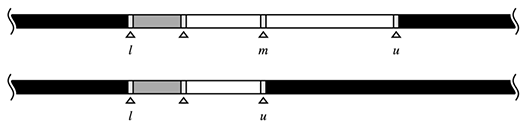
upper_bound型における範囲の更新

さて、ここからはupper_bound型を説明します。

• upper_bound型であり、現在注目しているf(a_m)が真である場合

mは解かもしれませんが、f(a_i)が真となる要素iはmよりも右側にまだあるかもしれません。ですので、右側をさらに詳しく探索します。

範囲を右閉半開区間として取ることにしたため、mは絞り込んだ範囲に含まれません。ですが心配することはありません。lower_bound型のときと同様に、最後には辻褄がちゃんと合います。

• upper_bound型であり、現在注目しているf(a_m)が偽である場合

求める解はmよりも左側にあります。ですので、左側をさらに詳しく探索します。

C++で実装すると以下のようになります。lower_bound型と見比べてみるのもよいでしょう。

  if (f(m)) {
    l = m;
  }
  else {
    u = m;
  }

まずはやってみよう

upper_bound型の場合

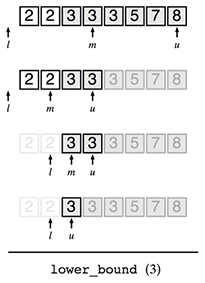
まずはやってみましょう。lower_bound型の二分探索の様子を見てみましょう。C++での実装は以下のようになります。

bool f(int x)
{
  return x >= 3;
}

int lower_bound() {
  int l = -1, u = 7;

  while (u - l > 1) {
    int m = (l + u) / 2;

    if (f(m)) {
      u = m;
    }
    else {
      l = m;
    }
  }

  /* 解は何? */
}

探索の様子を図示してみましょう。

うまく行きましたね! 範囲は最後に(1, 2]となりました(l = 1、u = 2)。範囲の定義からも、図からもuが答えとなることが分かります。

何故こんなにうまく行くのか考えてみましょう。

先ほどの節で説明した通り、lower_bound型の二分探索では現在注目しているf(a_m)が真であるとき、f(a_i)が真となる要素iはmよりも左側にまだあるかもしれないので、左側をさらに詳しく探索します(図を再掲します)。

範囲を右閉半開区間として取るため、mは絞り込んだ範囲に引き続き含まれます。例えばm未満に解がない場合、それ以降どのように探索されたとしても範囲は最終的に(m - 1, m]となります。

f(a_m)が偽であるとき、f(a_i)が真となる要素iは必ずmよりも右側にあります。そのため、右側をさらに詳しく探索します。

範囲を右閉半開区間として取るため、次の範囲(m, u]にmは含まれません。そもそもmは解の候補ではありませんし、lower_bound型の定義からm未満の要素に解はないはずです。そのため思い切って範囲から除くことができるのです。

upper_bound型の場合

次にupper_bound型の二分探索の様子も見てみましょう。

bool f(int x)
{
  return x <= 3;
}

int upper_bound() {
  int l = -1, u = 7;

  while (u - l > 1) {
    int m = (l + u) / 2;

    if (f(m)) {
      l = m;
    }
    else {
      u = m;
    }
  }

  /* 解は何? */
}

探索の様子を図示してみましょう。

...こちらは微妙ですね。解がlの位置にあります。どうしてこうなったか考えてみましょう。

まずf(a_m)が偽であるときのことを考えてみましょう。mより大きいiのa_iには解がありませんので、ばっさりと範囲から除くことができます(図は同じく、再掲です)。

さて、現在注目しているf(a_m)が真であるとき、それは解の候補となります。つまり、現在の要素、a_mは真に上限であるかもしれません。ですが、f(a_i)となる要素iはmよりも右側にまだあるかもしれないのです。右側を詳しく検索し続ける必要があるはそのためです。

範囲は右閉半開区間として取るのでした。次の期間は(m, u]となります。つまり、一時的に解の候補であるmは範囲から取り除かれます。

ではa_mが真の上限、つまり解であったとしましょう。a_{i ∈ (m, u]}には解がありませんよね。つまり、(m, u]のどのiの要素に対するf(a_i)はすべて偽になります。

そのため、これに続く探索は常に範囲の左側を残すように範囲を絞り続けることとなり、結局のところ範囲は(m, m + 1]となります。求める解はmです。

f(a_m)が解の候補であるけれども真の上限ではない場合、真の上限となるようなm'を有する区間(l', u']が(m, u]の範囲の中に必ずあるはずですので、やはり右側を詳しく探索します。真の上限となるm'が見つかった場合、範囲は(m', u']を経て(m', m' + 1]となります。この場合の解はm'となります。

本当にうまくいくの?

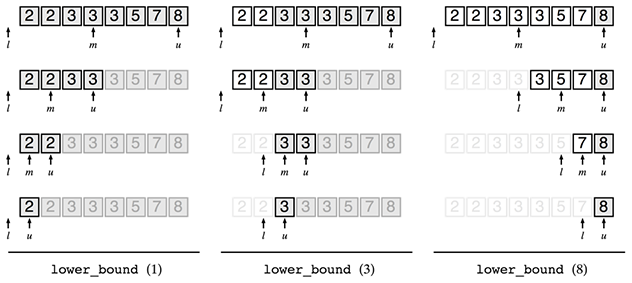
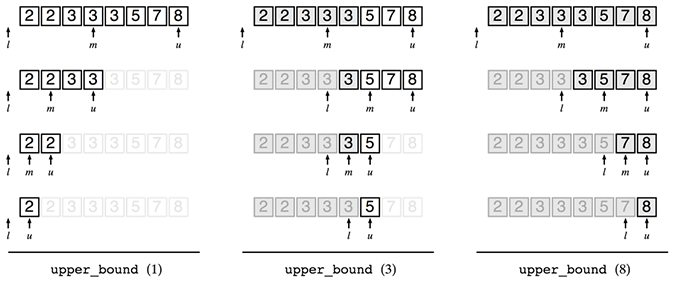
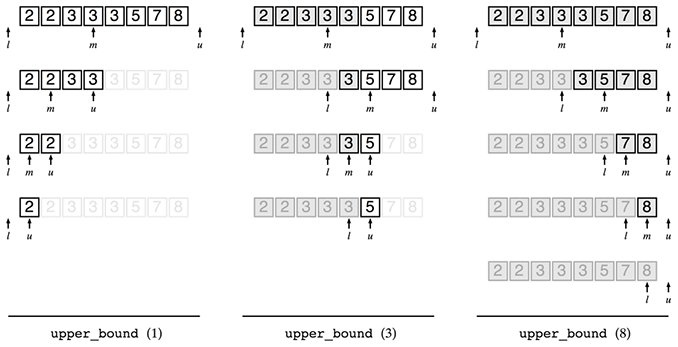
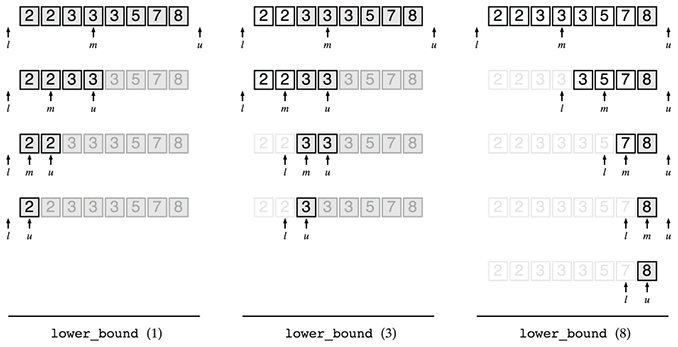
確信を得るために色々な場合の結果を見てましょう。以下はlower_bound型の二分探索を試した結果です。lower_boun型の二分探索の結果はuを見ればよいのでした。それぞれうまく行っているようです。

upper_bound型の二分探索も試してみましょう。

upper_bound型の二分探索の結果はlを見ればよいのでした。upper_bound (1)の戻り値が-1となってしまいました。これはなんでしょうか?

よく考えてみると、何れのiを用いても関数f(a_i)が真になることはありません。想定していない入力だったのでした。

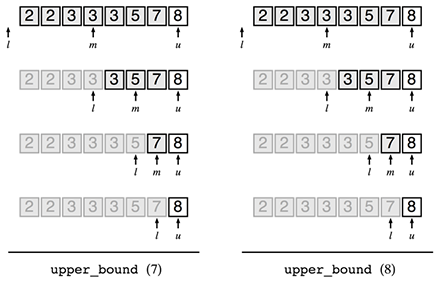
また、upper_bound (8)の結果がおかしいですね。この結果はupper_bound (7)の結果と同じようです。試しに比較してみましょう。

これはおかしいですね。どうしたらよいでしょう?

よりよくするために

まずupper_bound (1)について。これはそもそもupper_bound型の二分探索の定義がおかしかったのです。私たちは以下のように定義したのでした。

• upper_bound型
  • 関数f(a_i)が真となる最大のiを返す

イメージしていたのは以下のような図でした(再掲)。

これを以下のように改訂しましょう。

• upper_bound型
  • 関数f(a_i)が真となる最大のiを探索し、その次の要素を返す

upper_bound型の二分探索のイメージは以下となります。

数値を入れたときの図は以下のようになります。

これでupper_bound (1)の解釈も通るようになりました。以前のようにupper_bound型の探索でf(a_i)が真となる最大のiの要素の位置を知りたい場合はlを使うのではなく、u - 1を使うようにします。

これだとどうも分かり辛い、という方は冒頭に記載した楔型の図示をイメージするとよいと思います。

冒頭で少し触れたように、この方法は範囲を表す際によく使われる概念です。

STLのイテレータも楔型で考えると都合がよいものも多いです。std::begin()、std::end()、std::lower_bound()、std::upper_bound()、std::vector::insert()、std::vector::erase()等々...

例えばstd::vector::insert()は楔の位置に指定した要素群が挿入されると考えるとよいですし、std::vector::erase()も楔と楔の間の要素を削除すると考えるとよいかと思います。

話は少々脱線しましたが、次にupper_bound (8)について考えてみましょう。探索の初期範囲を(l^* - 1, u^*]ではなく、(l^* - 1, u^* + 1]としてみましょう。

図示すると以下のようになります。

上限を1つだけ大きくしただけですが、これだけで前の節での問題は不思議と解消されます。

もちろんlower_bound型もきちんと動作します。

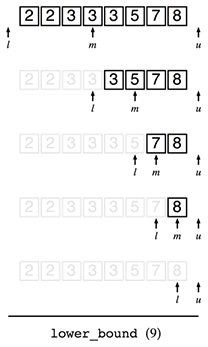
それに加え、lower_bound(9)のように解が存在しないも適切に表現できるようになります。

「f(u^* + 1)の挙動はそもそも未定義かもしれないじゃないか。もしかしたらアクセス違反するかも」と思うかもしれません。しかし、右閉半開区間を伴った二分探索ではmがu^* + 1となることがありません。そのため、アルゴリズム的な曖昧さはなく、関数f(x)を変更する必要もありません。

またそもそも関数f(x)を解が存在する範囲以上の入力に対応させ、ある程度余裕を持たせた初期範囲を設定するのも常套手段であるようです。

まとめ

このエントリでは二分探索で失敗をしないためのコツを考えてきました。

• 探索の型を見極める
  • lower_bound型か、upper_bound型か
• 初期範囲を決める
  • 右閉半開区間を用いる
  • 最低限(l^* - 1, u^* + 1]を設定する
• 反復の条件はu - l > 1が成立する間とする
• 中央値mを算出し、f(a_m)を評価する
• 評価の結果によって、範囲を更新する
  • lower_bound型でf(a_m)が真である場合、(l, m]を次の範囲とする
  • lower_bound型でf(a_m)が偽である場合、(m, u]を次の範囲とする
  • upper_bound型でf(a_m)が真である場合、(m, u]を次の範囲とする
  • upper_bound型でf(a_m)が偽である場合、(l, m]を次の範囲とする
• 探索の型によって解を選ぶ
  • lower_bound型である場合、関数f(a_i)が真となる最小のiはuである
  • upper_bound型である場合、関数f(a_i)が真となる最大のiはu - 1である

文章にすると意外に長いですが、実際には実装のテンプレートは決まっています。if文の中身を決定することが出来ればelse句は自然と決まりますので、コツを覚えなければならないのは二ヶ所です。

int {lower|upper}_bound() {
  int l = L, u = U;

  while (u - l > 1) {
    int m = (l + u) / 2;

    if (f(m)) {
      /* lower_bound型ではu = m; */
      /* upper_bound型ではl = m; */
    }
    else {
      /* lower_bound型ではl = m; */
      /* upper_bound型ではu = m; */
    }
  }

  /* lower_bound型ではreturn u; */
  /* upper_bound型ではreturn u - 1; */
}

範囲の更新の部分を思い出すのは簡単です。lower_bound型であるなら、以下の図をちょいちょいと書くだけです(図は再々掲)。

何れの型にしても、f(a_m)が真となるような図を書くのがポイントのようです。

奥深い二分探索

このエントリはCompetitive Programming Advent Calendar 2015の12/16日分のエントリとして記載しました。

私はこのエントリに記載したコツを使うことによって随分迷わなくなりましたが、二分探索の世界は実に奥深く、様々な「必勝法」が存在し、それに関する議論はいつも尽きないようです。

• にぶたん
• にぶたん談義

上位コーダーによる記事はシンプルにまとめられています。よく引用されるエントリには必ず目を通しましょう。

• 2012-07-03 - cafelier@SRM - TopCoder部
  • @kinabaさんによるエントリ
• 二分探索と三分探索 - komiyamの日記
  • @kou_miyamさんによるエントリ

プログラミングコンテストチャレンジブックの存在を忘れてはいけません。本エントリで記載した右閉半開区間を用いるアイデアはこの書籍を読んで得た知識です。プログラミングコンテストチャレンジブックでの二分探索のアプローチは@kinabaさんのアプローチに近いように感じています。

また、私は「ビット逐次決定型」と無理矢理名付けていますが、中央値を求めるような反復を行わず上位ビットから決定していく手法は、二分探索の議論において必ず言及されるようです。二分探索を違った視点から眺めることができますので、ご一読をお勧めします。

• @hirose_golfさんによるツィートとその実装例
• @Mi_Sawaさんによるツィートと実装例

また、@hirose_golfさんによる手法は本エントリで取ったアプローチと同様にlower_bound型とupper_bound型を設計段階で意識したアプローチとなっています。しかしながら、lower_bound型とupper_bound型を明確に区別するように紹介しましたが、そのような説明をする記事は少ないように感じます。少し考えるとupper_bound型はf(a_i)の否定(つまり! f(a_i))が真となる最小のiを探す問題、つまりlower_bound型に置き換えることができるからかなあと考えています。